a) Bestimmen sie die Gleichung der Tangente an dem Graphen der Funktion f mit
F(x)=\( x^{3} \) -3x +1 an der Stelle x0=1
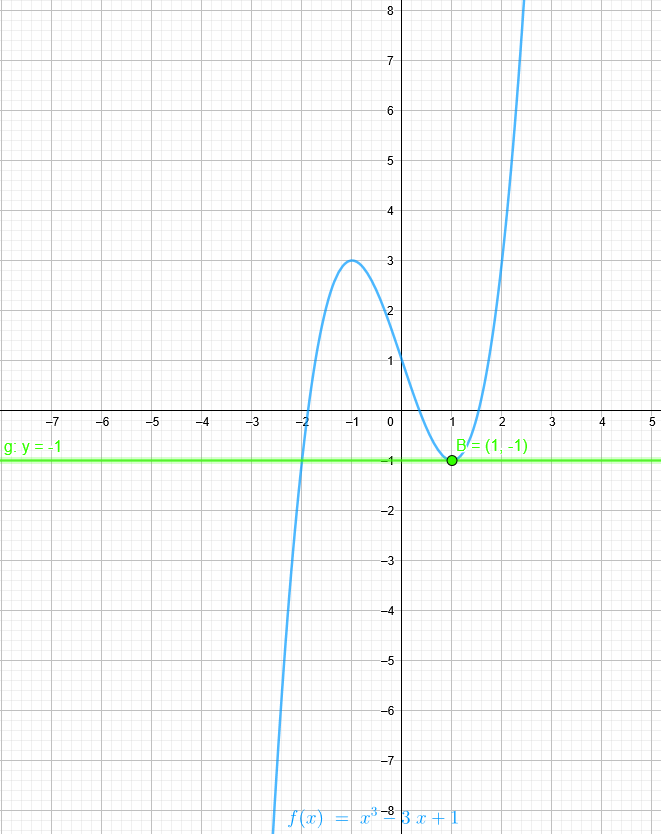
F(1)= \( 1^{3} \) - 3*1 +1 = -1
F´(x)= 3\( x^{2} \) - 3
F´(1)= 0
B(1|-1)
\( \frac{y-(-1)}{x-1} \) = 0
\( \frac{y+1}{x-1} \) = 0
y = - 1
b) Berechnen sie den Wert für a, für den diese Tangente durch den Ursprung geht:
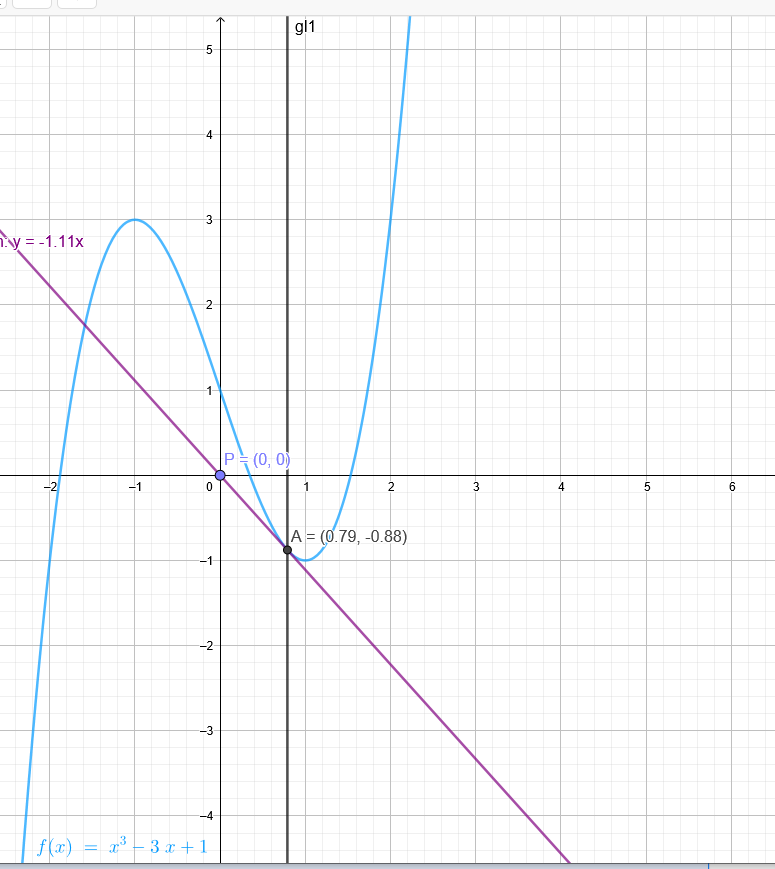
P(0|0)
\( \frac{y}{x} \) = m = F´(x)
y= (3\( x^{2} \) - 3)*x=3x^3-3x Dieses nun mit F(x) gleichsetzen:
3x^3 - 3 x = \( x^{3} \) - 3 x +1
2x^3=1
x^3=\( \frac{1}{2} \)
x₁ ≈ 0,79→y_1=....
F´( x₁)=...
Tangentengleichung aufstellen.