Hm,
zu den Grundlagen
siehe https://www.geogebra.org/m/fdmmvvma
>Drehung von O aus Richtung P betrachtet im Uhrzeigersinn < ?
Drehung von S, wohl oder?
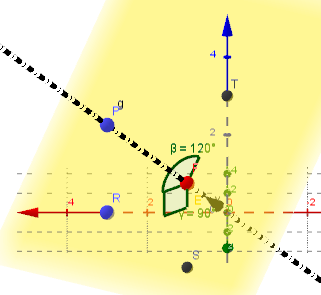
wir drehen R zurück nach S um 90° um Achsenvektor v=(1,1,1)/sqrt(3)T
\(\small R_{90°} \, := \, \left(\begin{array}{rrr}\frac{1}{3}&\frac{1}{3} \; \left(-\sqrt{3} + 1 \right)&\frac{1}{3} \; \left(\sqrt{3} + 1 \right)\\\frac{1}{3} \; \left(\sqrt{3} + 1 \right)&\frac{1}{3}&\frac{1}{3} \; \left(-\sqrt{3} + 1 \right)\\\frac{1}{3} \; \left(-\sqrt{3} + 1 \right)&\frac{1}{3} \; \left(\sqrt{3} + 1 \right)&\frac{1}{3}\\\end{array}\right)\)
S:=R90° R = \( \, \left(1, \sqrt{3} + 1, -\sqrt{3} + 1 \right)\)
im Uhrzeigersinn
\(\small R_{-120°} \, := \, \left(\begin{array}{rrr}0&1&0\\0&0&1\\1&0&0\\\end{array}\right)\)
T= R-120° R = (0,0,3)
Alle Punkte liegen in einer Ebene und drehen sich um den Achsenfixpunkt
F=v ((v R) / v²) = (1,1,1)