Aufgabe:
Gegeben sind die Funktionen f und g. Drücken Sie den Inhalt der beschriebenen Fläche mit a2 aus und brechnenen Sie sie mit einem Integral.
Fläche 2: Begrenzt von den Graphen f und g
Problem/Ansatz: Ich weiß, dass es die Frage schon einmal gibt, aber da kommt laut meiner Lehrerin das falsche Ergebnis raus. Könnte mir das jeamnd vorrechnen die anderen Afugaben habe ich auch verstanden. Hier muss 16/3 rauskommen.
Also 2 a ) Fläche 2 danke
Text erkannt:
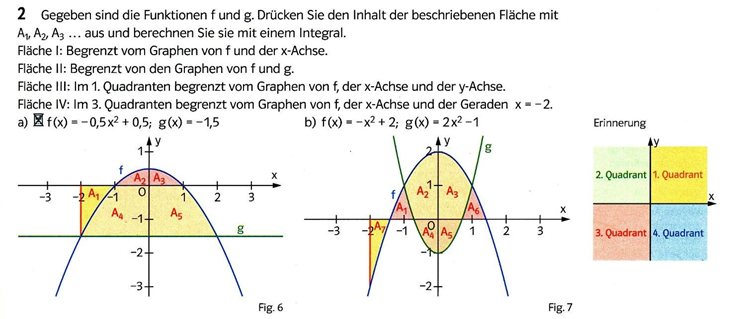
2 Gegeben sind die Funktionen \( f \) und \( g \). Drücken Sie den Inhalt der beschriebenen Flăche mit \( \mathrm{A}_{1}, \mathrm{~A}_{2}, \mathrm{~A}_{3} \ldots \) aus und berechnen Sie sie mit einem Integral. Fläche I: Begrenzt vom Graphen von \( f \) und der \( x \) -Achse. Fläche II: Begrenzt von den Graphen von \( f \) und \( g \). Fläche III: \( \operatorname{lm} \) 1. Quadranten begrenzt vom Graphen von \( \mathrm{f}, \) der \( \mathrm{x} \) -Achse und der \( \mathrm{y} \) -Achse. Fläche IV: Im 3. Quadranten begrenzt vom Graphen von f, der x-Achse und der Geraden \( x=-2 \).
a) \( \mathbb{Z} f(x)=-0,5 x^{2}+0,5 ; g(x)=-1,5 \quad \) b) \( f(x)=-x^{2}+2 ; g(x)=2 x^{2}-1 \quad \) Erinnerung