Funktionenschar untersuchen. Nullstellennormale, Ortskurve etc

Question

Aufgabe: Funktionenschar

Problem/Ansatz:

Kann mit jemand bei der d);e);f) helfen?

Text erkannt:

11. Gegeben ist die Funktionenschar \( f_{a}(x)=2 x \). ax
Untersuchen Sie \( \mathrm{f}_{\mathrm{a}} \) für \( \mathrm{x} \rightarrow \pm \infty \)
c) Bestimmen Sie die Gleichung der Nullstellennormalen
d) Ein achsenparalleles Rechteck mit einer Ecke im Ursprung und der gegenüberliegenden \( P_{a}\left(x_{a} \mid f\left(x_{a}\right)\right) \)
e) Bestimmen Sie mit dem Formansatz \( E(x)=(b x+c) \) ax \( d i e \) Koeffizientan Stammfunktion von \( f_{a} \). Bestimmen Sie den Inhalt der Fläche unter \( f_{a} \) über \( \left[-\frac{a}{2} ; 0\right] \). Hat die insgesamt unter \( f_{a} \) im 3 . Quadranten liegende Fläche einen endlichen
f) Zeigen Sie, dass die Ortskurven der Extrema und der Wendepunkte Ursprungsgeraden sind Unter welchem Winkel schneiden sie sich?

Comments

Möchte den Fragetitel zu :“ Funktionenschar untersuchen“ ändern

---

Da war (ist vielleicht immer noch) sonst so einiges in der Rechtschreibung ziemlich verkehrt.

V.a. ist der umgewandelte Text bei weitem nicht vollständig.

Verstehst du "achsenparalleles Rechteck"?

Kannst du das als Kommentar mal skizzieren?

Answer 1

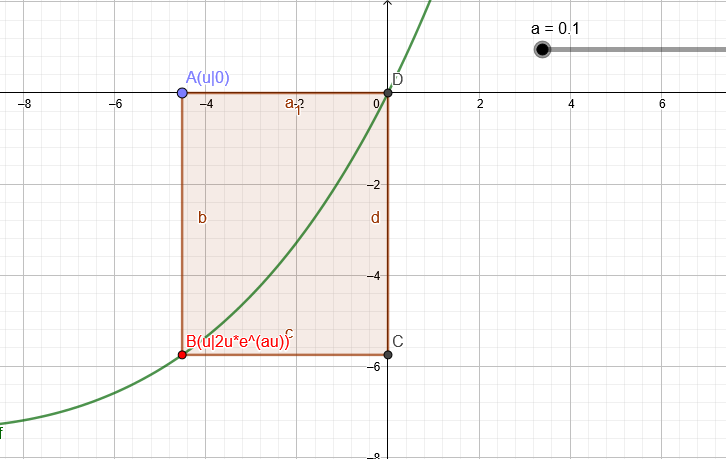
d) Ein achsenparalleles Rechteck mit einer Ecke im Ursprung und der gegenüberliegenden im 3.Quadranten auf f_a soll maximalen Inhalt haben. Ermitteln sie den Punkt \( P_{a}\left(x_{a} \mid f\left(x_{a}\right)\right) \)

f(x)=2x*\( e^{a·x} \)

A(u)=u*2u*\( e^{a·u} \)=2\( u^{2} \)*\( e^{a·u} \)

A´(u)=4u*\( e^{a·u} \)+2\( u^{2} \)*\( e^{a·u} \)*a

2u*\( e^{a·u} \)+\( u^{2} \)*\( e^{a·u} \)*a=0

\( e^{a·u} \)*(2u+a*\( u^{2} \))=0      \( e^{a·u} \)≠0

2u+a*\( u^{2} \)=0

u*(2+au)=0

u₁=0   Rechteck wird zu einem Punkt

u₂=-\( \frac{2}{a} \)

\( P_{a}\left(-\frac{2}{a} \mid 2 \cdot\left(-\frac{2}{a}\right) \cdot e^{a \cdot\left(-\frac{2}{a}\right)}\right) \rightarrow P_{a}\left(-\frac{2}{a} \mid\left(-\frac{4}{a}\right) \cdot e^{-2}\right) \rightarrow P_{a}\left(-\frac{2}{a} \mid-\frac{4}{a \cdot e^{2}}\right) \)