f '' (x) = 2·a·x·(x2 + 3·a) / (x2 - a)3
Für a>0 hat f '' nur die Nullstelle x=0 (mit Vorzeichenwechsel) → W(0|0)
für a<0 hat f '' die Nullstellen x=0 , x= ± √ (-3a) [ jeweils mit VZW]
→ W1 (0|0), W2,3 (± √(-3a) | ±3/4·√(-3a) )
Wegen der Symmetrie zum Ursprung liegen letztere alle auf der Ursprungsgeraden
mit der Steigung Δy/Δx = 3/4
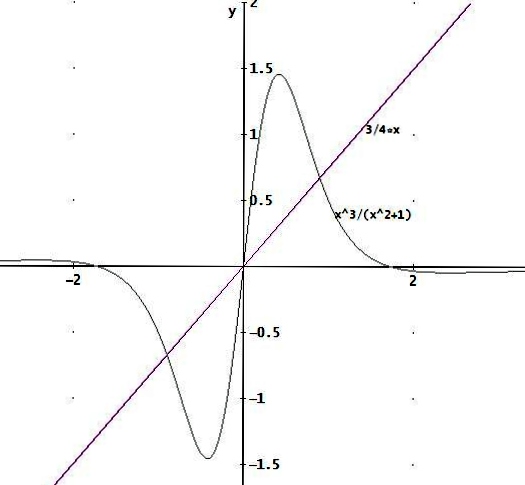
Ortskurve: y = 3/4 x
Beispielgraph mit a = -1
Gruß Wolfgang