findet ihr eventuell ein Fehler?

Question

Aufgabe:

… Hallo,

Ich habe eine Probleme mit einer Aufgabe und zwar, glaube ich habe die Höhe falsch berechnet. Findet ihr vielleicht den Fehler. I ch hoffe ihr könnt die Schrift lesen.

Problem/Ansatz:

… Um die Breite eine Baches zu bestimmen berechnen Lukas und Sophia am Ufer einer Standliene ST der Länge 29 m aus. Von jedem der beide Eckpunkte der Standlinie aus peilen sie einen Baum B am anderen Bachufer an und messen die Winkel Alpha=52 und bete 41 Grad. Berechnen Sie die Höhe die Bachbreite H.

Comments

Findet ihr einen Fehler?

:-)

Answer 1

Was du b genannt hast, liegt gegenüber von Winkel mit 52°.

Du musst also statt mit 41° mit 52° rechnen.

Gibt dann am Ende h=15m.

Comments

Aber im Dreieck SFB gibt es keine 52 Grad ? Oder meinst du 19,05 ist auch falsch?

---

Ich meinte das Dreieck STB.

Statt 19,05 gibt es dann 22,9

---

Ah jetzt verstehe ich sie. Aber warum soll ich denn den gegenüber liegenden wegen nehmen wen die Formel a/sin Alpha = b/sin beta = c/sin Gamma.

---

In der Formel ist immer:

eine Seite durch sin des gegenüberliegenden Winkels

Answer 2

Text erkannt:

Ein anderer Lösungsweg :
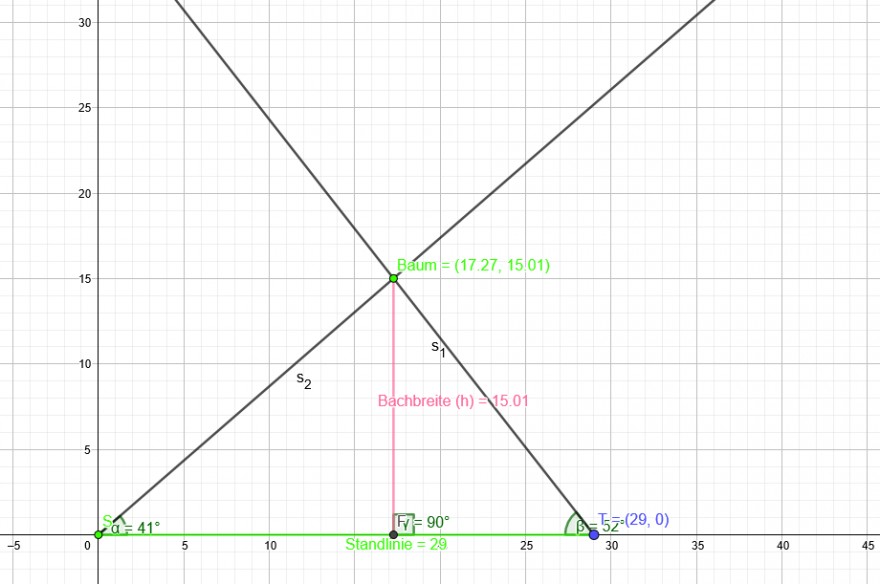
\( \tan 41^{\circ}=\frac{h}{\overline{S F}} \rightarrow \rightarrow \overline{S F}=\frac{h}{\tan 41}=\frac{h}{0,869} \)
\( \tan 52^{\circ}=\frac{h}{\overline{F T}} \)
\( \overline{S F}+\overline{F T}=29 \)
\( \overline{F T}=29-\overline{S F} \)
\( \tan 52^{\circ}=\frac{h}{29-\overline{S F}}=\frac{h}{29-\frac{h}{0,869}} \)
\( 1,28=\frac{h}{29-\frac{h}{0,869}} \)
\( h \approx 15,01 \)

Comments

Vielen Dank ich bin auch auf 15,01m gekommen gerade.

Könnten sie sagen ob 19,05 stimmt?

---

In der Zeichnung kommt auch 15,01 m raus. Somit ist 19,05m falsch.