Aufgabe:

Text erkannt:
1. Grenzwerte von Funktionen
Gegeben sind die Funktionen
\( f: x \rightarrow \frac{3}{x-2} \)
\( g: x \rightarrow \frac{1}{x^{2}-9} \)
\( \mathrm{h}: \mathrm{x} \rightarrow 2+\frac{1}{\mathrm{x}} \)
Folgende Aufgabenstellungen sind zunächst für die Funktion \( \mathrm{f} \), dann für die Funktion \( \mathrm{g} \) und schließlich für die Funktion h zu bearbeiten:
a) Bestimmen Sie den maximalen Definitionsbereich der Funktion.
b) Wie verhält sich die Funktion für \( x \rightarrow \infty \) und \( x \rightarrow-\infty ? \)
Geben Sie die beiden Grenzwerte für \( x \rightarrow \infty \) und für \( x \rightarrow-\infty \) und die Gleichung der Asymptote \( g \) an, der sich die Funktion annähert.
c) Wie verhält sich die Funktion an ihrer Definitionslücke / an ihren Definitionslücken? Geben Sie (falls vorhanden) die Gleichungen der senkrechten Asymptoten an den Polstellen an.
Problem/Ansatz:
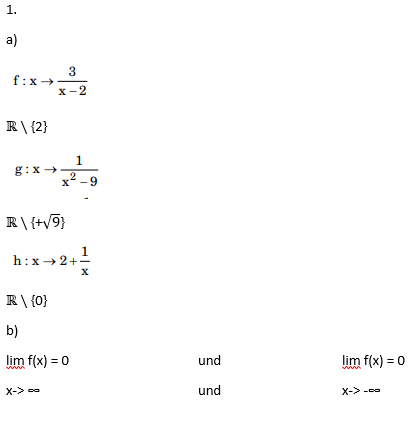
Text erkannt:
1
a)
\( f: x \rightarrow \frac{3}{x-2} \)
\( \mathbb{R} \backslash\{2\} \)
\( g: x \rightarrow \frac{1}{x^{2}-9} \)
\( \mathbb{R} \backslash\{+\sqrt{9}\} \)
\( \mathrm{h}: \mathrm{x} \rightarrow 2+\frac{1}{\mathrm{x}} \)
\( \mathbb{R} \backslash\{0\} \)
b)
\( \lim f(x)=0 \quad \) und \( \quad \lim f(x)=0 \)
\( \begin{array}{lll}x->\infty & \text { und } & x->-\infty\end{array} \)
Text erkannt:
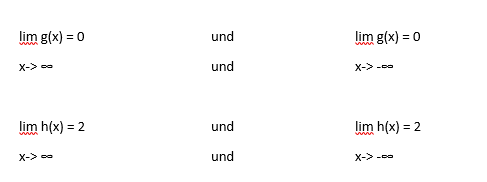
\( \lim \limits_{\lim } g(x)=0 \)
und \( \quad \lim \limits_{i} g(x)=0 \)
in \( x->\infty \)
\( \lim h(x)=2 \quad \) und \( \quad \lim h(x)=2 \)
\( x->\infty \)
und \( \quad x->-\infty \)
c) Ich verstehe nicht, was man hier machen soll, also durch Null Teilen kann man ja nicht, weshalb dort doch einfach nichts ist?
Sind die anderen Aufgaben mathematisch korrekt aufgeschrieben?