Komplexe Zahlen: Kartesische Koordinaten ↔ Polarkoordinaten. z₁=1/2(i+√3) und z₂=2i

Question

Gegeben seien
$$ z_{1}=\frac{1}{2}(\sqrt{3}+i) \text { und } z_{2}=2 i $$

a) Skizzieren Sie \( z, \) und \( z_{2} \) in der Gaußschen Zahlenebene. (Hinweis: \( \sqrt{3} \approx 1,73 \) )

b) Schreiben Sie beide Zahlen in Polarkoordinaten. Überprüfen Sie Ihre Umrechnung durch Messen in der Zeichnung.

c) Benutzen Sie die Polarkoordinatendarstellung, un das Produkt \( z_1 · z_2 \) zu berechnen.

d) Überprüfen Sie Ihr Ergebinis, indem Sie das Produkt aus \( z_1 \) und \( z_2 \) direkt in kartesischer Darstellumg berechnen und erst danach in Polarkoordinaten umrechnen.

e) Tragen Sie das Produkt \( z_1 · z_2 \) in die Gaußsche Zahlenebene ein.

Ansatz:
Aus den kartesischen Koordinaten \( x \) und \( y \) einer komplexen Zahl \( z=x+i y \) erhält man ihre Polarkoordinaten durch \( r=[z]=\sqrt{x^{2}+y^{3}} \) und \( \phi =a r g(z)=\arctan \frac{y}{x} \).

Aus den Polarkoordinaten einer komplexen Zahl \( z = r(\cos \phi + i \sin \phi \) erhält man ihre kartesischen Koordinaten durch \( x=r·\cos \phi \) und \( y=r·\sin \phi \).

Wie geht man bei der Aufgabe vor? Man kann ein Koordinatensystem als 360° sehen (nicht mathematisch ausgedrückt nur als Gedanke). Ein Vektor wird eingezeichnet. Man liest ab, welche Koordinaten der Vektor hat, z.B. 3i+1

1 auf dem Realteil von z [Re z] (x-Achse) und 3 auf dem Imaginärteil von z [Im z] (y-Achse)

φ = arg (z) = arctan (1/3).

Beachte: Es heisst z1=1/2(√(3) + i) und z2=2i.

Lösungsversuch:

Ich bitte um Kontrolle meiner Lösungen. Da es für mich ein neues Thema ist, bin ich mir nicht sicher und benötige daher Unterstützung.

a)
√3≈1,73
1/2*(1,73+i)=0,866+1/2i=z₁
2i=z₂

b)
Vektoren: ("|-Zeichen" steht für Trennung von oberen und unteren Vektor)

u=(0,87|0,5)
v=(0|2)

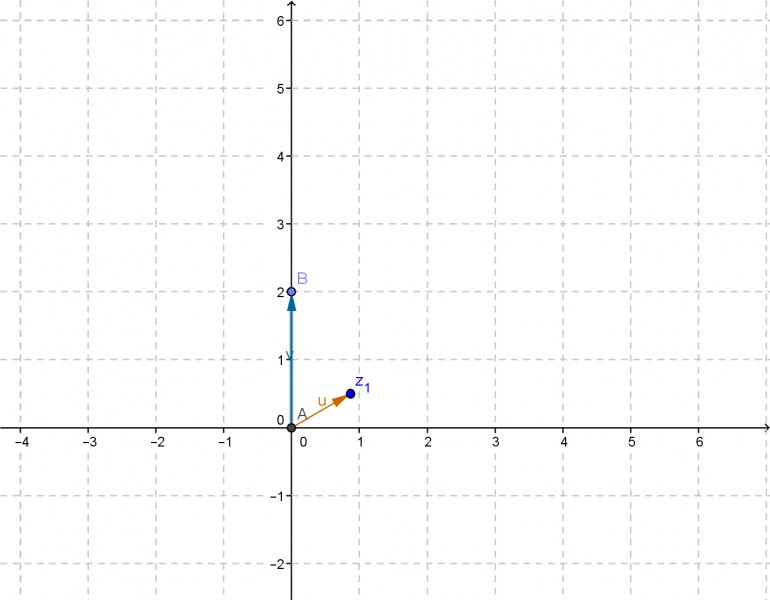
c) Polarkoordinaten z₁*z₂:
\( r=|z|=\sqrt{x^{2}+y^{2}} \) und \( \varphi=\arg (z)=\arctan \frac{y}{x} \)
\( r_{1}=\left|z_{1}\right|=\sqrt{0,866^{2}+0,5^{2}} \quad \) und \( \quad \varphi=\arg \left(z_{1}\right)=\arctan \frac{0,87}{0,5} \)
\( r_{2}=\left|z_{2}\right|=\sqrt{0^{2}+2^{2}} \quad \) und \( \quad \varphi=\arg \left(z_{2}\right)=\arctan \frac{0}{2} \)
oder Vektoren multiplizieren? \( \left(\begin{array}{c}{0,87} \\ {0,5}\end{array}\right) *\left(\begin{array}{l}{0} \\ {2}\end{array}\right)= \)

Wurzeln ausrechnen:

r₁=|z₁|=1
r₂=|z₂|=2

|z₁|*|z₂|=1*2=2

x=r₁*cosφ und y=r₁*sinφ

x=r₂*cosφ und y=r₂*sinφ


x=1*cos(0,87|0,5) und y=1*sin(0,87|0,5)

x=2*cos(0|2) und y=2*sin(0|2)

oder

x=1*cos(0,87) und y=1*sin(0,5)

x=2*cos(0) und y=2*sin(2)

Comments

Du hast

z1 = 1/2(√3 + i) richtig

gezeichnet.
In der Aufgabenstellung sehe ich aber
z1= 1/2(√(3+i) ) also das i  auch noch unter der Wurzel. Kann das sein?
Dann wären ja alle folgenden Rechnungen verkehrt.

---

Ich denke, dass es richtig ist. Ich stecke bei b) fest. Wie komme ich auf die Polarkoordinaten mit π? Man geht vom Punkt aus immer links bis zur (x-Achse bzw. Re z-Achse). Vielleicht könnt ihr euch mithilfe des Bildes mehr darunter vorstellen und mir Tipps geben, da es für mich ein neues Thema ist und ich nicht weiß wie man diese Aufgaben berechnet.

z₂=2i
r=2
arg(z)=2π/2 (?)

z₁=0,866+1/2i
r=0,866^2+0,5^2

z₂=2i
r=2
arg(z₂)=0,5*π

0,5*π=90°=1,5708 Bogenmaß

z₁=0,866*0,5i
r=0,99998
arg(z₁)=0,5*π

0,16667*π=30°=0,52361 Bogenmaß

Ist das korrekt?

zu c)
Benutzen Sie die Polarkoordinatendarstellung, um das Produkt z₁ · z₂ zu berechnen.

Also,

z₁ =0,866+1/2i

z₂ =2i

arg(z₁)=0,16667*π·arg(z₂)=0,5*π 

0,16667*π·0,5*π=3π/2

oder

30°·90°=270° (oder 4.71238898038469 Bogenmaß)

---

a) ist ok.

b) z2 hast du glaub ich mehrmals.

Polardarstellung von 2i ist 

z₂=2i 

r=2 
arg(z₂)=0,5*π 

z2 = 2*e^{i*0.5π}       Polardarstellung. Normalerweise lässt man das π  stehen, zumindest bei schönen Zahlen.

r(z1) = r(√3 / 2 + 1/2 i)

= √(3/4 + 1/4) = 1

arg(z1)= arctan( 1/2 / √3/2) = arctan( 1/√3) =30° = π/6

z1 liegt ja im 1. Quadranten! Du musst daher nicht noch π addieren! 

---

x=r*cos φ und y=r*sin φ .

x=0.99998*cos 0,16667*π=
y=0.99998*sin 0,16667*π=

x=0,5*cos 0,5*π=
y=0,5*sin 0,5*π=

Richtige Formeln?



PS: Antwort von Lu habe ich erst gesehen, nachdem ich das hier geschrieben habe.

---

Also, ist c) korrekt, oder? Und wie sieht es mit den Formel bei d) aus?

Statt 30° kann man also π/6 schreiben. Wieder etwas dazu gelernt.

---

Bist du auch noch bei b)?

jein. Du hast einen Rundungsfehler drinn und bei z2 für r = 0.5 statt r= 2 . Ich geb dir mal die ungerundeten Werte nochmals an.

x=r*cos φ und y=r*sin φ . 

x=0.99998*cos 0,16667*π 

ungerundet

x=1*cos(π/6)
y=0.99998*sin 0,16667*π 

y=1*sin(π/6)

x=2*cos 0,5*π 
y=2*sin 0,5*π 

Soweit alles ok. Mathematisch nicht mehr weiterrechnen für b). 

---

Stimmt, ich habe statt 2; 0,5 geschrieben. Und statt 0,16667 hast du π/6 schrieben. O.K. Und mithilfe der Lösungen aus b) kann man d) berechnen, stimmt's? Oder habe ich bereits c) gelöst?

Ich werde zur besseren Übersicht alles zusammenfassen!

---

a)

√3≈1,73 
1/2*(1,73+i)=0,866+1/2i=z₁ 
2i=z₂
 

b)

z₂=2i 
r=2
arg(z₂)=0,5*π 
z2 = 2*e^i*0.5π

r(z1) = r(√3 / 2 + 1/2 i)

=√(3/4 + 1/4) = 1

arg(z1)= arctan( 1/2 / √3/2) = arctan( 1/√3) =30° = π/6

x=r*cos φ und y=r*sin φ .  
x=0.99998*cos 0,16667*π
y=0.99998*sin 0,16667*π

ungerundet
x=1*cos(π/6)
 y=1*sin(π/6)

x=2*cos 0,5*π  
y=2*sin 0,5*π

c) 
Benutzen Sie die Polarkoordinatendarstellung, um das Produkt z₁ · z₂ zu berechnen.

z₁ =0,866+1/2i
z₂ =2i

arg(z₁)=0,16667*π·arg(z₂)=0,5*π

0,16667*π·0,5*π=3π/2 

oder 

30°·90°=270° (oder 4.71238898038469 Bogenmaß)

d)
x=1*cos(π/6)=1
y=1*sin(π/6)=0,009138395=i
z₁=1+i

x=2*cos 0,5*π=1  
y=2*sin 0,5*π=0,054803665=i
z₂=1+i

Answer 1

Und mithilfe der Lösungen aus b) kann man c) berechnen, stimmt's?

Ja. Das soll man da tun.

Geht aber einfacher mit dem, was ich unter Polardarstellung verstehe:

z2 = 2*e^i*0.5π       

z1 = 1*e^{i*π/6}    Polardarstellung.

z1 * z2 =  2*e^i*0.5π * 1*e^{i*π/6}

=2*(e^{iπ(1/2 + 1/6)} = 2*e^{i4π/6}

= 2(cos(120°) + i sin (120°)) = -1 + i*√3.

d) Kontrolle:

z1*z2 = 1/2(√3 + i) *2i = √3i + i^2 = -1 + i*√3

e) Eintragen in die komplexe Zahlenebene ist nun nicht mehr schwer.

Kontrolle. Multipliziert man eine Zahl z1 mit einer Zahl z2= r*e^{iPHI}, so wird die Länge von z1 mit r multipliziert und der resultierende Zahlenvektor noch um den Winkel PHI gedreht.

Hier also z1 bekommt doppelte Länge und wird um π/2 = 90° im Gegenuhrzeigersinn gedreht.