Hallo,
um die sogenannten Spurpunkte zu bestimmen, muss jeweils eine der drei Kordinaten \(x\), \(y\) und \(z\) zu \(0\) werden. Die Geradengleichung ist$$g: \quad \vec x = \begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}-2\\ -3\\ 4\end{pmatrix} + k \cdot \begin{pmatrix}-1\\ -5\\ 2\end{pmatrix}$$Für den Spurpunkt der YZ-Ebene muss das \(x=0\) sein. Daraus folgt$$x = 0 = -2 + k_{yz} \cdot (-1) \implies k_{yz} = -2$$Setzt man dieses \(k_{yz}\) in \(g(k)\) ein, so erhält man den Spurpunkt$$g(k_{yz}) = \begin{pmatrix}-2\\ -3\\ 4\end{pmatrix} + (-2) \cdot \begin{pmatrix}-1\\ -5\\ 2\end{pmatrix} = \begin{pmatrix}0\\ 7\\ 0\end{pmatrix}$$wie man sieht, ist hier auch der Z-Koordinate \(=0\). Hier fallen zwei Spurpunkte zusammen.
Genauso wird dann noch der zweite Spurpunkt in der ZX-Ebene berechnet. Folgendes Bild zeigt das nochmal anschaulich
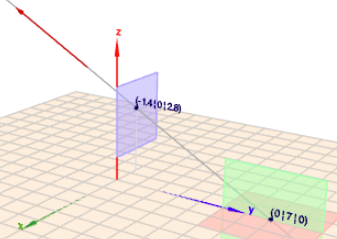
(klick auf das Bild, dann öffnet sich Geoknecht3D)