Umschreibung einer Wurzel

Question

Hallo. Ich bin gerade am Lösen einer Aufgabe und im Lösungsweg des Dozenten war dieser Rechenschritt. Ich verstehe nicht wie der linke Term in den rechten umgeschrieben wurde. Ich habe beim Lösen vieler unterschiedlicher Aufgaben gemerkt, dass so eine Umschreibung bei Wurzeln diesen Umfangs üblich sind.

Kann mir daran jemand bitte eine Regelmäßigkeit bzw. Gesetzmäßigkeit  erklären, sodass ich auch in Zukunft solche Sachen eigenständig erkennen und umsetzen kann?

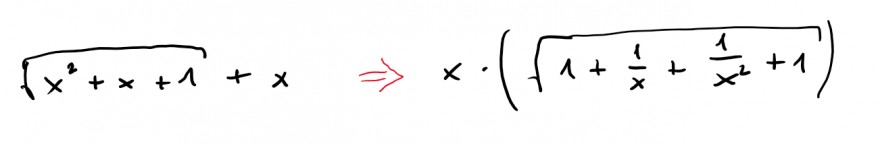
Text erkannt:

\( \sqrt{x^{2}+x+1}+x \Rightarrow x \cdot\left(\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}+1}\right) \)

Danke für Eure Mühen.

Answer 1

Hallo,

Du schreibst:

$$\sqrt{x^{2}+x+1}+x \Rightarrow x \cdot\left(\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}+1}\right) $$

so wie es da steht, ist das falsch. Setze für \(x\) einfach mal eine \(1\) ein, dann stände da \(\sqrt 3 + 1 \Rightarrow 2\). Du meinst wahrscheinlich $$\sqrt{x^{2}+x+1}+x \Rightarrow x \cdot\left(\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}}+1\right)$$Die Umformung geht so:$$\begin{aligned} \sqrt{x^{2}+x+1}+x &= \sqrt{x^2\left(1 + \frac 1x + \frac 1{x^2}\right)} + x \\ &= \sqrt{x^2} \cdot \sqrt{1 + \frac 1x + \frac 1{x^2}} + x \\&= x \sqrt{1 + \frac 1x + \frac 1{x^2}} + x \\&= x \left( \sqrt{1 + \frac 1x + \frac 1{x^2}} + 1\right)\end{aligned}$$

Comments

Besten Dank, habs verstanden!