Wenn es um den geringsten Abstand von zwei jeweils windschiefen Geraden im dreidimensionalen Raum geht, wie erstellt …

Question

Wenn es um den geringsten Abstand von zwei jeweils windschiefen Geraden im dreidimensionalen Raum geht, wie erstellt …

2 Antworten

Ein anderes Problem?

Werner-Salomon · Answer 1 · 2021-02-17T11:40:19+0000

Hallo,

Willkommen in der Mathelounge!

Ich kann ja nicht einfach die erste Ableitung der Differenz der beiden Geraden nehmen. Dafür gäbe es ja auch zu viele Variablen.

Es gibt genau zwei Variablen und danach kann man auch ableiten. Nehme zwei Geraden $$g: \quad \vec x = \vec p_g + s\cdot \vec r_g \\ h: \quad \vec x = \vec p_h + t\cdot \vec r_h $$der Abstand soll minimal werden$$|g(s) - h(t)| \to \min$$heißt auch, dass das Quadrat $e$ des Abstands minimiert werden soll - also$$e(t,s) = (\vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h)^2 \to \min $$und das leite man nach $s$ und $t$ ab:$$\frac{\partial e}{\partial s} = 2(\vec p_g - \vec p_h + s \vec r_g- t \vec r_h)\vec r_g \to 0\\ \frac{\partial e}{\partial t} = 2(\vec p_g - \vec p_h + s \vec r_g - t \vec r_h)\vec r_h \to 0$$und das ist ein lineares Gleichungssystem mit zwei Unbekannten. In dieser Form$$\begin{pmatrix} \vec r_g^2 & -\vec r_h \vec r_g \\ \vec r_g \vec r_h & -\vec r_h^2 \end{pmatrix} \begin{pmatrix} s\\t \end{pmatrix} = \begin{pmatrix} (\vec p_h - \vec p_g) \vec r_g\\ (\vec p_h - \vec p_g) \vec r_h \end{pmatrix}$$

Beantwortet 17 Feb 2021 von Werner-Salomon

Wie ist das Quadrat $e$ definiert?

das soll das Abstandsquadrat sein. $e$ ist so definiert, wie es da steht:$$e=|g(s) - h(t)|^2 = (\vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h)^2$$

Auch wenn ich das Quadrieren der Differenz zum Quadrat nicht verstehe.

Na ja - viel zu verstehen gibt es da gar nicht. Das ist eher ein Trick, um sich die Wurzellei zu sparen. Sei der Abstand $a$$$a = |g(s) - h(t)|$$dann ist das ausgeschrieben:$$\dots = \sqrt{(\vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h)^2}$$wenn man das jetzt ableitet, bekommt man$$a' = \frac{\left((\vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h)^2\right)'}{2\sqrt{(\vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h)^2}} \to 0$$und das ist nur genau dann $=0$, wenn der Zähler $=0$ ist. Und der Zähler ist identisch mit dem Ausdruck oben in meiner Antwort - also mit der Ableitung von $e$ dem Abstandsquadrat.

Auf 'mathematisch' heißt das: Da das Quadrieren für positive Argumente eine streng monoton stetig steigende Funktion ist, ist dort ein Extremwert auch eine Extremwert des Arguments (oder so ähnlich)

Bzw.: wenn $a^2 \lt b^2$ dann gilt auch $|a| \lt |b|$

Und das Minus in der zweiten Geradengleichung, zwischen Stütz- und Richtungsvektor, ist aufgrund des Minus in der Differenz, oder?

Ja sicher $$\begin{aligned} g(s) - h(t) &= (\vec p_g + s\cdot \vec r_g) - (\vec p_h + t\cdot \vec r_h) \\&= \vec p_g + s\cdot \vec r_g - \vec p_h - t\cdot \vec r_h\end{aligned}$$

Kommentiert 17 Feb 2021 von Werner-Salomon

verstehe ich doch noch nicht den Übergang der jeweils abgeleiteten e-Quadrat-Funktion ... zu dem linearen Gleichungssystem

... das ist Übung ;-) Es steht oben und unten genau das gleiche, nur eben in einer anderen Form$$\begin{aligned}\frac{\partial e}{\partial s} = 2(\vec p_g - \vec p_h + s \vec r_g- t \vec r_h)\vec r_g &= 0\\ \frac{\partial e}{\partial t} = 2(\vec p_g - \vec p_h + s \vec r_g - t \vec r_h)\vec r_h &= 0 \\ &\Downarrow \\ (\vec p_g - \vec p_h)\vec r_g + s \vec r_g^2- t \vec r_h \vec r_g &= 0 \\ (\vec p_g - \vec p_h)\vec r_h + s \vec r_g\vec r_h - t \vec r_h^2 &= 0 \\ &\Downarrow \\ s \vec r_g^2- t \vec r_h \vec r_g &= (\vec p_h - \vec p_g)\vec r_g \\ s \vec r_g\vec r_h - t \vec r_h^2 &= (\vec p_h - \vec p_g)\vec r_h \\ \Downarrow \\ \begin{pmatrix} \vec r_g^2 & -\vec r_h \vec r_g \\ \vec r_g \vec r_h & -\vec r_h^2 \end{pmatrix} \begin{pmatrix} s\\t \end{pmatrix} &= \begin{pmatrix} (\vec p_h - \vec p_g) \vec r_g\\ (\vec p_h - \vec p_g) \vec r_h \end{pmatrix} \end{aligned}$$

Kommentiert 17 Feb 2021 von Werner-Salomon

Wenn man mit dem Rechnen mit Vektoren und Matrizen mehr vertraut ist, dann kann man auch eine $3\times 2$-Matrix $R$ definieren$$R = \begin{pmatrix} \vec r_g &\vec r_h\end{pmatrix}$$Weiter nenne ich die Differenz der Positionsvektoren $\vec p_h - \vec p_g = \Delta \vec p$ (achte auf die Reihenfolge von $g$ und $h$!)

und dann ist $e$ $$e = \left( - \Delta \vec p + R \begin{pmatrix} s\\ -t \end{pmatrix}\right)^2$$

die Ableitung von $e$ nach dem 'Vektor' $\begin{pmatrix} s&-t\end{pmatrix}^T$ ist dann$$ \vec e' = 2R^T \left( - \Delta \vec p + R \begin{pmatrix} s\\ -t \end{pmatrix}\right) \to 0 \\ \implies R^T R \begin{pmatrix} s\\ -t \end{pmatrix} = R^T \Delta \vec p$$.. ist wieder das gleiche wie oben ;-) und die Form eignet sich prima als Eingabe in ein Tabellenkalkulaionsprogramm, wie z.B. Excel oder LibreOffice.

Kommentiert 17 Feb 2021 von Werner-Salomon

Beziehungsweise setze ich das ja dann hier: $|g(s) - h(t)| $ ein...

Ja natürlich. Obiges lineares Gleichungssystem liefert Dir die Werte von $s_{\text{opt}}$ und $t_{\text{opt}}$ mit dem minmalen Abstand. Und $g(s_{\text{opt}})$ und $h(t_{\text{opt}})$ sind jeweils die Punkte auf den Geraden mit dem kleinsten Abstand zur jeweils anderen.

Der Betrag der Differenz $|g(s) - h(t)| $ ist dann dieser minimale Abstand. Und $e(s_{\text{opt}}, t_{\text{opt}})$ wäre eben das Quadrat dieses Abstands gewesen.

Rechne doch mal ein Beispiel durch:

$$g: \quad\vec x = \begin{pmatrix}-2\\ 2\\ 0\end{pmatrix} + s\begin{pmatrix}1\\ 0\\ 1\end{pmatrix} \\ h: \quad \vec x = \begin{pmatrix}3\\ -1\\ -1\end{pmatrix} + t\begin{pmatrix}0\\ 2\\ 1\end{pmatrix}$$

die Ergebnisse findest Du im Geoknecht3D. Klicke dazu auf das Bild.

Kommentiert 18 Feb 2021 von Werner-Salomon

Also ich verstrehe nicht ganz, was ich falsch mache. Egal wie oft ich die Aufgabe durchgehe, komme ich nicht auf die 3 LE. Allerdings finde ich meinen Fehler auch nicht. Es kann natürlich deswegen so sein, da ich ihren letzten Schritt:...

( $\begin{pmatrix} \vec r_g^2 & -\vec r_h \vec r_g \\ \vec r_g \vec r_h & -\vec r_h^2 \end{pmatrix} \begin{pmatrix} s\\t \end{pmatrix} = \begin{pmatrix} (\vec p_h - \vec p_g) \vec r_g\\ (\vec p_h - \vec p_g) \vec r_h \end{pmatrix}$ )

...doch nicht ganz nachvollziehen konnte und ich diesen übersprungen habe.

So leuchtet mir nicht ein, wie sie $s$ und $t$ so isolieren konnten um den Vektor:...

$ \begin{pmatrix} s\\t \end{pmatrix}$

...zu erstellen. Doch an sich dürfte das kein Hindernis sein. Gerade bei ihrem Beispiel kann man ja schon relativ zeitig die werte für $s$ und $t$ ablesen.

Kommentiert 18 Feb 2021 von Gast

So leuchtet mir nicht ein, wie sie $s$ und $t$ so isolieren konnten ...

Ok - mal ganz langsam. Die einzelnen Elemente des LGS sind:$$\vec r_g^2 = 1^2 + 0^2 + 1^2 = 2 \\ \vec r_h \vec r_g = 1 \cdot 0 + 0 \cdot 2 + 1 \cdot 1 = 1 \\ \vec r_h^2 = 0^2 + 2^2 + 1^2= 5 \\ \vec p_h - \vec p_g = \begin{pmatrix}5\\ -3\\ -1\end{pmatrix} \\ (\vec p_h - \vec p_g) \vec r_g = 5 \cdot 1 + (-3)\cdot 0 + (-1) \cdot 1= 4 \\ (\vec p_h - \vec p_g) \vec r_h = 5 \cdot 0 + (-3)\cdot 2 + (-1) \cdot 1= -7$$Macht alles zusammen$$\begin{pmatrix} 2& -1\\ 1& -5\end{pmatrix} \begin{pmatrix} s\\ t \end{pmatrix} = \begin{pmatrix} 4\\ -7 \end{pmatrix}$$verdoppele die zweite Zeile und ziehe sie von der ersten ab: $$0 s + 9t = 18 \implies t = 2$$Einsetzen in die zweite Gleichung des LGS gibt$$s - 10 = -7 \implies s = 3$$Jetzt in die Geradengleichungen einsetzen liefert die Werte für die Punkte $g(s=3)$ und $h(t=2)$.

Kommentiert 18 Feb 2021 von Werner-Salomon

Ja okay, das ist schlüssig.

Allerdings verstehe ich den Übergang vom vorletzten zum letzten Schritt hierbei:...

$\begin{aligned}\frac{\partial e}{\partial s} = 2(\vec p_g - \vec p_h + s \vec r_g- t \vec r_h)\vec r_g &= 0\\ \frac{\partial e}{\partial t} = 2(\vec p_g - \vec p_h + s \vec r_g - t \vec r_h)\vec r_h &= 0 \\ &\Downarrow \\ (\vec p_g - \vec p_h)\vec r_g + s \vec r_g^2- t \vec r_h \vec r_g &= 0 \\ (\vec p_g - \vec p_h)\vec r_h + s \vec r_g\vec r_h - t \vec r_h^2 &= 0 \\ &\Downarrow \\ s \vec r_g^2- t \vec r_h \vec r_g &= (\vec p_h - \vec p_g)\vec r_g \\ s \vec r_g\vec r_h - t \vec r_h^2 &= (\vec p_h - \vec p_g)\vec r_h \\ \Downarrow \\ \begin{pmatrix} \vec r_g^2 & -\vec r_h \vec r_g \\ \vec r_g \vec r_h & -\vec r_h^2 \end{pmatrix} \begin{pmatrix} s\\t \end{pmatrix} &= \begin{pmatrix} (\vec p_h - \vec p_g) \vec r_g\\ (\vec p_h - \vec p_g) \vec r_h \end{pmatrix} \end{aligned}$

...nicht ganz.Also wie man aus dem Gleichungssystem in diesem Fall eine Matrix aufbaut und s und t isoliert.

Kommentiert 18 Feb 2021 von Gast

Allerdings verstehe ich den Übergang vom vorletzten zum letzten Schritt hierbei ... nicht ganz.

Im Grunde findet da gar kein Übergang statt. Das sind nur zwei unterschiedliche Schreibweisen für die gleiche Sache. Ich mache es mal mit dem Zahlenbeispiel. Aus$$\begin{aligned} 2s - t &= 4 \\ s - 5t &= -7\end{aligned}$$wird in der Matrixschreibweise.$$\begin{pmatrix} 2& -1\\ 1& -5\end{pmatrix} \begin{pmatrix} s\\ t \end{pmatrix} = \begin{pmatrix} 4\\ -7 \end{pmatrix}$$Auf der linken Seite des linearen Gleichungssystems (LGS) steht die Multiplikation einer Matrix mit dem Vektor aus $s$ und $t$.

Das schriftlich zu erklären, ist irgendwie schwierig, weil es so einfach ist! Schau Dir mal dies Beispiel an oder hier ist das auch mit Zahlen erklärt, aber natürlich ist das egal, ob da Zahlen oder Variablen stehen.

Kommentiert 19 Feb 2021 von Werner-Salomon

würde ich dann tatsächlich beispielsweise die Vektoren.... subtrahieren?

Nein! das steht da auch nicht! Wenn Du das so schreibst $$\begin{pmatrix} \begin{pmatrix} 1\\0\\-1 \end{pmatrix}& - \begin{pmatrix} 0\\2\\1 \end{pmatrix}\\ \begin{pmatrix} 1\\0\\1 \end{pmatrix}& - \begin{pmatrix} 0\\4\\1 \end{pmatrix}\end{pmatrix} \begin{pmatrix} s\\ t \end{pmatrix} = \begin{pmatrix} \begin{pmatrix} -5\\0\\1 \end{pmatrix}\\ \begin{pmatrix} -5\\-6\\1 \end{pmatrix} \end{pmatrix}$$dann steht da $$\begin{pmatrix} 1\\0\\-1 \end{pmatrix} s -\begin{pmatrix} 0\\2\\1 \end{pmatrix} t = \begin{pmatrix} -5\\0\\1 \end{pmatrix} \\ \begin{pmatrix} 1\\0\\1 \end{pmatrix} s - \begin{pmatrix} 0\\4\\1 \end{pmatrix} t = \begin{pmatrix} -5\\-6\\1 \end{pmatrix}$$das wäre völlig äquivalent. Jetzt bleibt die Frage wie Du darauf kommst?

Kommentiert 19 Feb 2021 von Werner-Salomon

Ja, jetzt komme ich auch auf die Vektoren.

Äh - ja wie denn?? Die Vektoren aus Deinem Kommenatr vom 19.2 um 9:35 kann ich nicht zuordnen.

Allerdings ist mir noch etwas unklar, wie man eine solche Matrix dann löst.

Die Matrix löst man gar nicht. Gelöst wird das lineare Gleichungssystem (LGS). Ich hatte oben schon erwähnt, dass dies $$\begin{pmatrix} 2& -1\\ 1& -5\end{pmatrix} \begin{pmatrix} s\\ t \end{pmatrix} = \begin{pmatrix} 4\\ -7 \end{pmatrix}$$und dies $$\begin{aligned} 2s - t &= 4 \\ s - 5t &= -7\end{aligned}$$absolut das gleiche ist. Nur eben in einer anderen Schreibweise. Wenn das LGS mehr Unbekannten hätte, würde man es nach dem Gauß-Verfahren lösen.

So ein kleines Ding kann man (fast!) im Kopf rechnen. Hier bietet sich das Subtraktionsverfahren an. Multipliziere die zweite Gleichung mit $2$ und ziehe sie von der ersten ab:$$\implies 9t = 18 \implies t = 2$$das setzt man z.B. in die zweite Gleichung an, und löst nach $s$ auf:$$s - 5\cdot2 = -7 \implies s = 3$$

Kommentiert 21 Feb 2021 von Werner-Salomon

Ich muss mich nocheinmals entschuldigen. Ich habe, schätze ich, die falsche Frage gestellt.

Mein Problem war, dass ich praktisch nicht verstanden habe, wie sie mit den Vektoren umgehen. Beispielsweise an folgender Stelle:

$\vec r_g^2 = 1^2 + 0^2 + 1^2 = 2 \\ \vec r_h \vec r_g = 1 \cdot 0 + 0 \cdot 2 + 1 \cdot 1 = 1 \\ \vec r_h^2 = 0^2 + 2^2 + 1^2= 5 \\ \vec p_h - \vec p_g = \begin{pmatrix}5\\ -3\\ -1\end{pmatrix} \\ (\vec p_h - \vec p_g) \vec r_g = 5 \cdot 1 + (-3)\cdot 0 + (-1) \cdot 1= 4 \\ (\vec p_h - \vec p_g) \vec r_h = 5 \cdot 0 + (-3)\cdot 2 + (-1) \cdot 1= -7$

Ich glaube mein einziges wirkliches Problem war, dass ich nicht verstanden habe, wie sie, wenn ein vektor quadriert oder mit einem anderen Vektor multipliziert wird, die unterschiedlichen werte für x/y/z zu einer Zahl addieren, wie als würden sie diese Skalar-multiplizieren. Dafür würde mir allerdings kein Grund einfallen.

Kommentiert 21 Feb 2021 von Gast

... dass ich nicht verstanden habe, wie sie, wenn ein vektor quadriert oder mit einem anderen Vektor multipliziert wird, die unterschiedlichen werte für x/y/z zu einer Zahl addieren, ...

Das ist das Skalarprodukt. Wenn man zwei Vektoren hat, so kann man diese mit einander multiplizieren wie zwei Matrizen oder eine Matrix und einen Vektor. Vektor ist wie Matrix nur eben mit einer Spalte. Ist$$\vec v_1 = \begin{pmatrix}a\\ b\\ c\end{pmatrix}, \quad v_2 = \begin{pmatrix}x\\ y\\ z\end{pmatrix}$$so lautet das Skalarprodukt $s$ korrekt$$s = v_1^T \cdot v_2$$eine andere Schreibweise ist$$s = \left< v_1,\, v_2\right>$$man beachte das ${}^T$ beim ersten Vektor.. Das steht für 'transponiert'. Das ${}^T$ lässt man an dieser Stelle oft weg, da es 'selbstverständlich' ist.

Und ausgeschrieben ist es dann$$s = \begin{pmatrix}a & b&\ c\end{pmatrix} \cdot \begin{pmatrix}x\\ y\\ z\end{pmatrix} = a\cdot x + b \cdot y + c \cdot z$$Das Skalarprodukt ist immer eine Zahl also ein Skalar, daher der Name.

Kommentiert 22 Feb 2021 von Werner-Salomon

Ich dachte, das Skalarprodukt würde hinweise auf die Größe des Winkels geben.

man kann mit dem Skalarprodukt den Winkel zwischen zwei Vektoren berechen. Das ist aber nur eine klitzeklein Anwendung desselben.

Dennoch ist mir nicht klar, weshalb man das so macht.

Man 'macht' es eben nicht! Sondern es ergibt sich so. Du erinnerst Dich an unsere Ausgangsgleichung.$$e(s,t) = (s\cdot \vec r_g - t\cdot \vec r_h - \Delta \vec p)^2 $$Das $\vec p_h - \vec p _g$ habe ich mit $\Delta \vec p$ abgekürzt, sonst wird das folgende zu lang.

Das $e(s,t)$ soll minimiert werden. Auf die Wurzel, die der Betrag des Differenzenvektors wäre, hatten wir ja bereits verzichtet. Wenn das Quadrat minmal wird, ist auch die Wurzel minmal!

Ohne Vektorschreibweise stünde da$$e(s,t) = (sr_{gx} - tr_{hx}- \Delta p_x)^2 + (sr_{gy} - tr_{hy}- \Delta p_y)^2 + (sr_{gz} - tr_{hz}- \Delta p_z)^2$$ist das gleiche wie oben, nur eben ohne Vektorschreibweise. Jetzt nach $s$ ableiten:$$\frac{\partial e}{\partial s} = 2(sr_{gx} - tr_{hx}- \Delta p_x)r_{gx} + 2(sr_{gy} - tr_{hy}- \Delta p_y)r_{gy} + 2(sr_{gz} - tr_{hz}- \Delta p_z)r_{gz}$$Wieder ziemlich länglich aber auch nicht sonderlich kompliziert. Jetzt schaue Dir diesen Ausdruck mal genau an. Die $2$ ist ein konstanter Faktor vor jedem Summanden und der Rest sieht doch aus wie $$\dots = ax + by + cz$$das sieht aus, wie ein Skalarprodukt. Also könnte man es auch in Vektorschreibweise hinschreiben:$$\begin{aligned} \frac{\partial e}{\partial s} &=2 \begin{pmatrix} r_{gx}& r_{gy}& r_{gz}\end{pmatrix} \cdot \begin{pmatrix} sr_{gx} - tr_{hx}- \Delta p_x\\sr_{gy} - tr_{hy}- \Delta p_y \\sr_{gz} - tr_{hz}- \Delta p_z \end{pmatrix} \\ &= 2\vec r_g^T(s \vec r_g- t \vec r_h - \Delta \vec p) \end{aligned}$$und schon sind wir wieder bei dem Ausdruck, mit dem ich oben in meiner Antwort vom 17.2. angefangen habe.

D.h. der Einsatz von Vektoren führt lediglich zu einer verkürzten Schreibweise. Und dass sich dann zwischendurch Skalarprodukte bilden, ist ein logischer Prozess.

Kommentiert 22 Feb 2021 von Werner-Salomon

Aber weshalb ist das "Produkt zweier Vektoren" gleich dem "Skalar"?
Also wie kann es dasselbe sein, wie wenn ich einen der beiden Vektoren transformiere (transponiere) und ihn dann somit multiplizieren?

Schaue Dir bitte zunächst mal an, wie Matrizen-Multiplikation im Prinzip funktioniert, bevor Du hier weiter liest!

Eine Matrix habe $n$ Zeilen und $m$ Spalten. Dann sei sie eine $n \times m$-Matrix. Man kann nur zwei Matrizen $n_1 \times m_1$ und $n_2 \times m_2$ multiplizieren, wenn $m_1 = n_2$ ist. Ein Vektor ist nichts anderes wie eine Matrix mit einer Spalte.

Liegt also ein Vektor von $3 \times 1$ vor, so kann ich den nur mit einem anderen Vektor $3 \times 1$ multiplizieren, wenn ich einen von beiden transponiere - heißt ihn zu einen $1 \times 3$-Vektor machen. Z.B. $$\begin{pmatrix}1\\ 2\\ 3\end{pmatrix}^T = \begin{pmatrix}1& 2& 3\end{pmatrix}$$Transponiere ich den ersten der beiden ergibt das das Skalarprodukt$$\begin{pmatrix}1\\ 2\\ 3\end{pmatrix}^T \cdot \begin{pmatrix}4\\ 5\\ 6\end{pmatrix} = \begin{pmatrix}1& 2& 3\end{pmatrix} \begin{pmatrix}4\\ 5\\ 6\end{pmatrix} = 1\cdot 4 + 2\cdot 5 + 3\cdot 6$$Das Ergebnis ist ein Skalar (eine Zahl) - daher der Name.

Transponiert man den zweiten der Vektoren im Produkt, so erhält man das sogenannte Dyadische Produkt:$$\begin{pmatrix}1\\ 2\\ 3\end{pmatrix} \cdot \begin{pmatrix}4\\ 5\\ 6\end{pmatrix}^T = \begin{pmatrix}1\\ 2\\ 3\end{pmatrix} \cdot \begin{pmatrix}4& 5& 6\end{pmatrix} \\ \quad = \begin{pmatrix}1\cdot 4& 1\cdot5& 1\cdot6\\ 2\cdot 4& 2\cdot5& 2\cdot6\\ 3\cdot 4& 3\cdot5& 3\cdot6\end{pmatrix}$$und das ist eine quadratische Matrix.

Beziehungsweise habe ich ein zu einfaches Verständnis von Vektoren und Matrizen

... eher ein zu kompliziertes! ;-) Vektoren und Matrizen sind im Grunde nur tabellarische Anordnungen von Zahlen, oder anderen Elementen.

... verstehe ich nicht den Zusammenhang zwischen dem Skalarprodukt und dieser Gleichung:
$\frac{\partial e}{\partial s} = 2(sr_{gx} - tr_{hx}- \Delta p_x)r_{gx} + 2(sr_{gy} - tr_{hy}- \Delta p_y)r_{gy} + 2(sr_{gz} - tr_{hz}- \Delta p_z)r_{gz}$

Substituiere:$$sr_{gx} - tr_{hx}- \Delta p_x = a\\ sr_{gy} - tr_{hy}- \Delta p_y = b\\ sr_{gz} - tr_{hz}- \Delta p_z = b$$und weiter$$r_{gx} = x, \quad r_{gy}=y, \quad r_{gz} = z$$dann steht doch da:$$2(sr_{gx} - tr_{hx}- \Delta p_x)r_{gx} + 2(sr_{gy} - tr_{hy}- \Delta p_y)r_{gy} + 2(sr_{gz} - tr_{hz}- \Delta p_z)r_{gz} \\ \space = 2ax + 2by + 2cz \\\space = 2(ax + by + cz) \\ \space = 2 \cdot \begin{pmatrix}a& b& c\end{pmatrix} \cdot \begin{pmatrix}x\\ y\\ z\end{pmatrix}$$was das Skalarprodukt zweier Vektoren ist. Es ist wirklich nur eine andere Schreibweise!

Kommentiert 25 Feb 2021 von Werner-Salomon

Es tut mir wirklich leid, dass ich bei diesem Thema eventuell etwas "schwerfällig" bin.

Gut, dann ziehe ich das mal ganz anders auf. Nehmen wir doch mal einen Vekor im Raum:

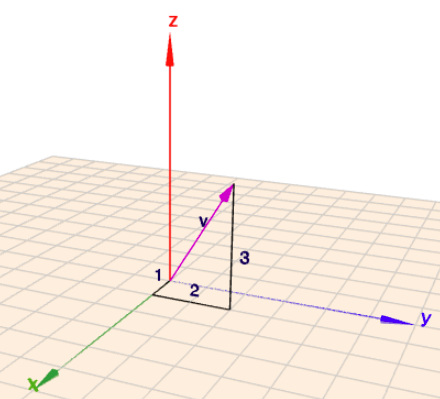
$$v = \begin{pmatrix}1\\ 2\\ 3\end{pmatrix}$$Dieses Ding 'Vektor' ist eine gerichtete Größe. In der Physik werden damit z.B. Geschwindigkeiten, Kräfte oder auch Feldlinien beschrieben.

Wenn Du aber wissen möchtest wie lang der Vektor ist, also wissen möchtest wie schnell ein Auto, wie groß die Kraft oder wie ausgeprägt eine Feldlinie an einer bestimmten Stelle ist, dann benötigst Du die Länge $l$ des Vektors. Und diese Länge berechnet sich (nach Pythagoras!) aus der Wurzel der Quadratesumme der Koordinaten. Hier:$$l =|\vec v| = \sqrt{1^2 + 2^2 +3^2}$$Wenn Du den Pythagoras da nicht siehst, versuche es bitte mal mit einem Vektor in der Ebene!

Diese Quadratesumme ist aber identisch zum Skalarprodukt des Vektors mit sich selbst:$$|\vec v| = \sqrt{\vec v^2}= \sqrt{\vec v^T \cdot \vec v} \\ \quad= \sqrt{\begin{pmatrix}1& 2& 3\end{pmatrix} \cdot \begin{pmatrix}1\\ 2\\ 3\end{pmatrix}} =\sqrt{1^2 + 2^2 +3^2} $$In der Praxis wird dieses ${}^T$ beim ersten Vektor oft weg gelassen. Du wirst sicher häufiger $\vec a \vec b$ lesen als $\vec a^T \vec b$ lesen. Aber gemeint ist immer das zweite.

In unseren konkreten Fall ist ein Vektor $\vec d$ von einem Punkt der Geraden zu einem Punkt auf der anderen Geraden, die Differenz dieser beiden Punkte:$$\vec d = \vec g(s) - \vec h(t) = s\vec r_g - t\vec r_h - \Delta \vec p$$Was nun interessiert, ist die Länge von $\vec d$. Es soll ja die Stelle gefunden werden, an der die Länge von $\vec d$ und damit der Abstand zwischen den Geraden minimal wird. Folglich betrachten wir$$|\vec d| = \sqrt{\vec d^2}$$Und da das Maximum der Wurzel auch das Maximum des Quadrats ist, betrachten wir der Einfachheit halber nur das Quadrat:$$|\vec d|^2 = \vec d^2 = e(s,t)$$Und die Berechnung der Quadratesumme ändert sich dadurch ja nicht. Also ist$$e(s,t) = d_x^2 + d_y^2 + d_z^2$$Und jetzt setze für $d_x$, $d_y$ und $d_z$ wieder die Ausdrücke $s\vec r_{gx} - t\vec r_{hx} - \Delta \vec p_{x}$, $s\vec r_{gy} - t\vec r_{hy} - \Delta \vec p_{y}$ und $s\vec r_{gz} - t\vec r_{hz} - \Delta \vec p_{z}$ ein. Und damit kommst Du zu dieser Gleichung oben.

beziehungsweise:
$(\vec r_g - \vec r_h)^2 $ == $ \begin{pmatrix} (r_{gx} - r_{hx})^2\\(r_{gy} - r_{hy})^2 \\(r_{gz} - r_{hz})^2 \end{pmatrix} $

Nein - die Gleichung ist Unsinn! $(\vec r_g - \vec r_h)^2 $ ist das Quadrat der Länge der Differenz von $\vec r_g$ und $\vec r_h$. Und eine Länge, bzw. das Quadrat einer Länge, ist kein Vektor!

$(\vec r_g - \vec r_h)^2 $
≠:
$(r_{gx} - r_{hx})^2+(r_{gy} - r_{hy})^2 +(r_{gz} - r_{hz})^2 $

Nein - das ist gleich. Das ist simpler Pythagoras!

Bitte bitte schau Dir noch mal die Matrizenmultiplikation an. In der Addition werden die Koordinaten der Vekoren jeweils addiert $$\begin{pmatrix}1\\ 2\\ 3\end{pmatrix} + \begin{pmatrix}4\\ 5\\ 6\end{pmatrix} = \begin{pmatrix}1 +4\\ 2+5\\ 3+6\end{pmatrix}$$Bei der Muliplikation ist das nicht(!) so.

So eine Multiplikation:$$\begin{pmatrix}1\\ 2\\ 3\end{pmatrix} \cdot \begin{pmatrix}4\\ 5\\ 6\end{pmatrix} = \text{undefiniert!}$$gibt es gar nicht. Es gibt aber das Skalarprodukt$$\begin{pmatrix}1& 2& 3\end{pmatrix} \cdot \begin{pmatrix}4\\ 5\\ 6\end{pmatrix} = 1\cdot 4 + 2\cdot 5 + 3\cdot 6$$Und genauso ist$$\begin{pmatrix}a& b\\ c& d\end{pmatrix} \cdot \begin{pmatrix}u& v\\ w& x\end{pmatrix} = \begin{pmatrix}au+bw& av+bx\\ cu+dw& cv+dx\end{pmatrix}$$Jedes Element des Produkts rechts ist das Skalarprodukt eines Zeilenvektors der ersten Matrix mit eine Spaltenvektor der zweiten Matrix$$\begin{array}{cc}{}& \begin{pmatrix}u\quad& \quad{\color{red}v}\\ {w}\quad& \quad{\color{red}x}\end{pmatrix}\\ \begin{pmatrix}{\color{red}a}& {\color{red}b}\\ c& d\end{pmatrix}& \begin{pmatrix}{\color{grey}au+bw}& {\color{red}av+bx}\\ {\color{grey} cu+dw}& {\color{grey}cv+dx}\end{pmatrix}\end{array}$$Also hier ist $$\begin{pmatrix}a& b\end{pmatrix} \cdot \begin{pmatrix}v\\ x\end{pmatrix} = av+bx$$Schau Dir mal ein Video über Matrizenmultiplikation an.

Kommentiert 26 Feb 2021 von Werner-Salomon

Wenn es um den geringsten Abstand von zwei jeweils windschiefen Geraden im dreidimensionalen Raum geht, wie erstellt …

2 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: