Bestimmen Sie mit Hilfe des Differentialquotienten alle \( a \in \mathbb{R} \), sodass die Funktion \( g(x)=(2 x-a)|x-3| \) auf ganz \( \mathbb{R} \) differenzierbar ist.
\( g(x)=(2 x-a) \cdot \sqrt{(x-3)^{2}} \)
\( g \cdot(x)=2 \cdot \sqrt{(x-3)^{2}}+\frac{(2 x-a) \cdot 2 \cdot(x-3)}{2 \cdot \sqrt{(x-3)^{2}}}=2 \cdot \sqrt{(x-3)^{2}}+\frac{(2 x-a) \cdot(x-3)}{\sqrt{(x-3)^{2}}}= \)
\( =\frac{2 \cdot(x-3)^{2}+(2 x-a) \cdot(x-3)}{\sqrt{(x-3)^{2}}}=\frac{4 x^{2}-18 x+18-a x+3 a}{\sqrt{(x-3)^{2}}} \)
\( 4 x^{2}-18 x+18-a x+3 a=0 \)
\( 4 x^{2}-18 x-a x=-18-3 a \)
\( 4 x^{2}-(18+a) \cdot x=-18-3 a \mid: 4 \)
\( x^{2}-\frac{18+a}{4} \cdot x=\frac{-18-3 a}{4} \)
\( x_{1}=\frac{18+a}{8}+\sqrt{\frac{-18-3 a}{4}+\left(\frac{18+a}{8}\right)^{2}} \)
\( x_{2}=\frac{18+a}{8}-\sqrt{\frac{-18-3 a}{4}+\left(\frac{18+a}{8}\right)^{2}} \)
\( \sqrt{\frac{-18-3 a}{4}+\left(\frac{18+a}{8}\right)^{2}}=0 \)
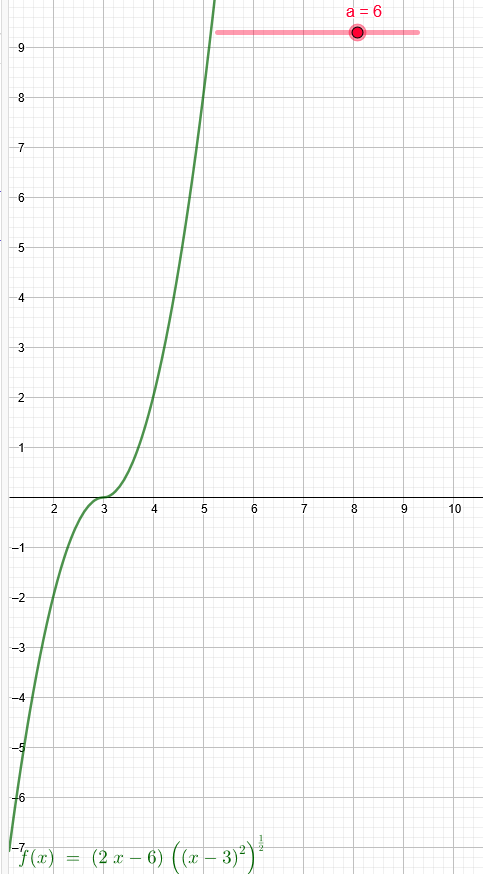
\( a=6 \)
\( g(x)=(2 x-6) \cdot \sqrt{(x-3)^{2}} \)