die Aufgabe mit der Buche hätte ich genau so gerechnet wie Du:
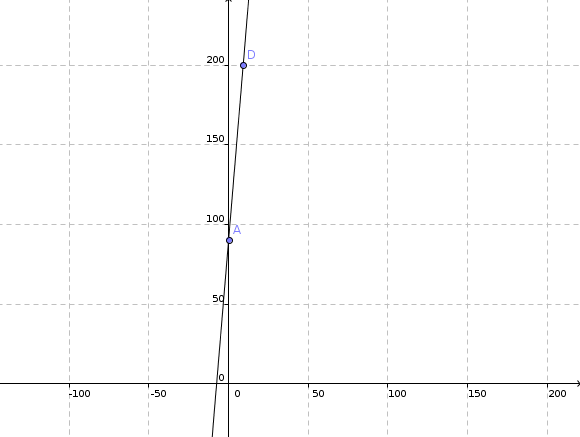
f(x) = 12x + 90
f(x) = 200 = 12x + 90
12x = 110
x = 110/12 = 55/6 ≈ 9,167
Zweite Aufgabe:
Wenn Bierschaum 10 cm hoch ist und pro 15 sek sinkt der Level um 9%. es soll alles pro Minute umgerechnet werden.
Hier hätte ich eine exponentielle Funktion aufgestellt f(x)=10x0,64t
In 15 sek sinkt der Level um 9% (* 0,91), also in einer Minute 0,914 ≈ 0,6857
Da weichen unsere Ergebnisse ein wenig voneinander ab.
Dann hätte ich aber ebenso geschrieben:
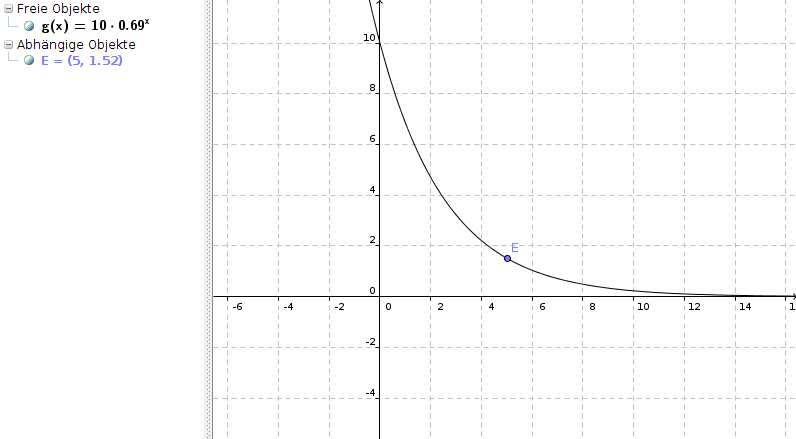
f(t) = 10 * 0,6857t
Dann wären wir zum Beispiel nach 5 Minuten bei
f(5) = 10cm * 0,68575 ≈ 1,5159cm
(Punkt E im Graphen)
Besten Gruß