Gleichung einer Ebene erstellen die von anderen Ebenen eingegrenzt wird

Question

Upload failed: [object Object]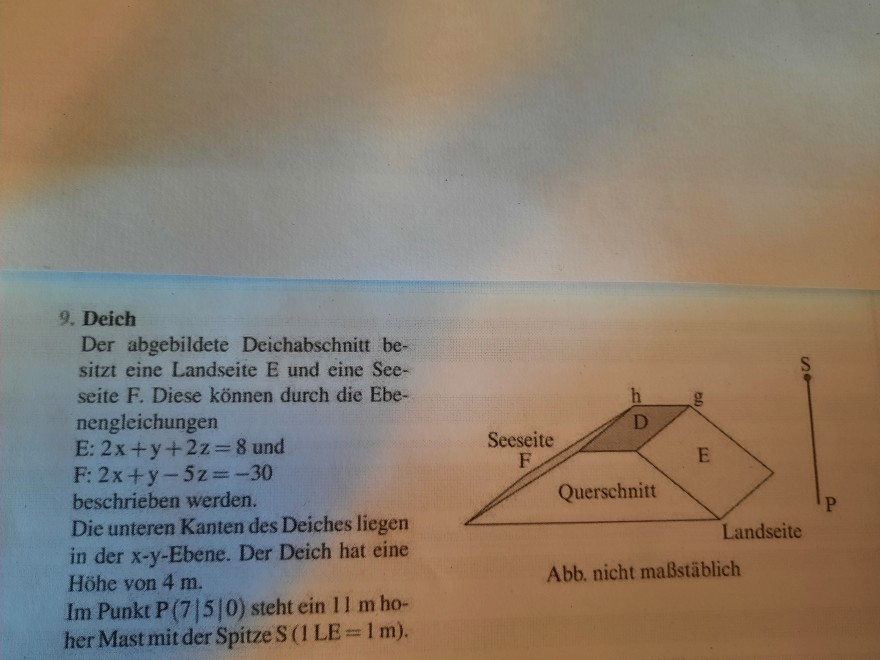

Text erkannt:

9. Deich Der abgebildete Deichabschnitt besitzt eine Landseite \( E \) und eine Seeseite F. Diese können durch die Ebenengleichungen
E: \( 2 x+y+2 z=8 \) und
\( F: 2 x+y-5 z=-30 \)
beschrieben werden. Die unteren Kanten des Deiches liegen in der \( x-y \) -Ebene. Der Deich hat eine Hóhe von \( 4 \mathrm{~m} \). Im Punkt \( P(7|5| 0) \) steht ein 11 m hoher Mast mit der Spitze S \( (1 L E=1 \mathrm{~m}) \)

Die Deichkrone liegt in der Ebene D und wird von den geraden g und h begrenzt, die jeweils zu den anliegenden Ebenen E und F gehören wie Stelle ich D durch eine Ebenengleichung dar ?

Comments

Ok Z=4 Das habe ich verstanden aber wie komme ich jetzt zu der Ebenengleichung für D ? Und wie kommen die Geradengleichungen zustande ?

Answer 1

Alle Punkte von D liegen auf der Höhe 4 über der xy-Ebene, also

D :  z=4.

Die begrenzenden Geraden sind

(0;0;4) + t*(1;-2;0) und
(0;-10;4) + t*(1;-2;0)

Comments

Ok Z=4 Das habe ich verstanden aber wie komme ich jetzt zu der Ebenengleichung für D ? Und wie kommen die Geradengleichungen zustande ?

---

z=4, das ist schon die Ebenengleichung.

Und die beiden Geraden sind die Schnitte von D

mit den anderen beiden Ebenen.