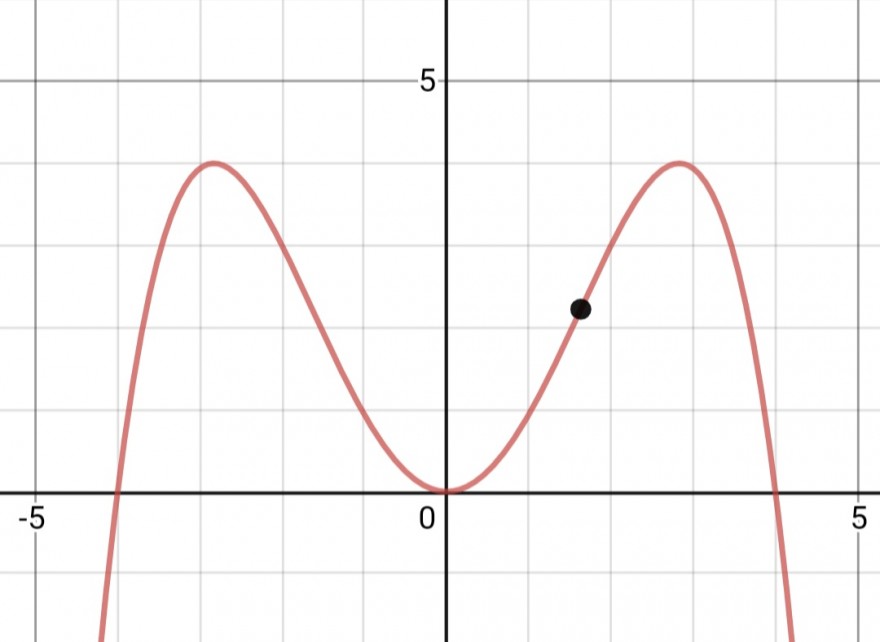
Der Graph einer ganz rationalen Funktion (4. Grades) verläuft achsensymmetrisch zur y-Achse und durch den Koordinatenursprung.
Daraus folgt
f(x)=ax^4+cx^2
Die y-Koordinate der Wendepunkte beträgt Zweizweineuntel.
Also yW=20/9.
f'(x)=4ax^3+2cx
f''(x)=12ax^2+2c → gleich Null setzen
x^2=-c/(6a) in f(x) einsetzen.
20/9 = a*c^2/(36a^2)-c^2/(6a)= c^2/(36a)-c^2/6a=-5/36 *c^2/a
c^2=-16a bzw. a=-c^2/16
Die Maßzahl des vom Graphen mit der x-Achse im ersten Quadranten eingeschlossenen Flächenstücks beträgt Achtachtfünfzehntel.
Wir brauchen also die positive Nullstelle.
f(x)=ax^4+cx^2=0
ax^2=-c
-c^2/16 *x^2 =-c
x^2=16/c
xN=+√(16/c)
Eine Stammfunktion:
F(x)=-c^2/16 *x^5/5 + cx^3/3
Integral von Null bis zur positiven Nullstelle:
F(xN)=128/15
128/15=-c^2/16 *xN^5/5 + cxN^3/3 |*15
128 = -3c^2/16*xN^5+5cxN^3
128=( -3c^2/16*(16/c)^2+5c*(16/c))*√(16/c)
128=(-48+80)*√(16/c)
4=√(16/c)
c=1
a=-1/16
f(x)=-1/16 *x^4 + x^2
:-)