Ich hege Zweifel an der Richtigkeit der 1. Aufgabenstellung
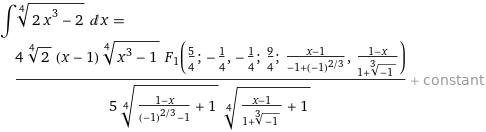
Vielleicht ist folgendes gemeint
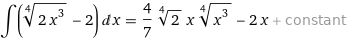
Die zweite Aufgabe ist recht einfach. Du sieht im Zähler bis auf einen Faktor von 3 die Ableitung des Nenners. Multipliziere also den Zähler mit 3 und Multipliziere das gesamte Integral dafür mit 1/3. Dann kannst du einfach über Umkehrung der Kettenregel integrieren
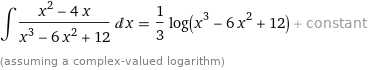
Rechnungen wurden mit Wolframalpha durchgeführt.