Stochastik: Porzellangefäße 1. und 2. Wahl

Question

Aufgabe:

Bei der Produktion von Porzellangefäßen sind erfahrungsgemäß 15% der Gefäße wegen schlechter Form, 20% wegen unsauberer Farbe und 25% wegen ungleichmäßiger Oberfläche nicht 1. Wahl. Ein Porzellangefäß ist 2. Wahl, wenn es genau eine der drei Kontrollen nicht besteht. Der Rest ist Ausschuss.

a) Fertige ein vollständiges Baumdiagramm für den Prüfungsablauf an.
b) Wie groß ist der Anteil der Gefäße 1. Wahl?
c) Wie häufig gibt es 2. Wahl?
d) Wie viel Ausschuss gibt es?

Problem/Ansatz:

Kann mir jemand helfen, ich bin in Stochastik so schlecht

Answer 1

Ereignisse:

E1 :  Porzellangefäßen 1. Wahl
E2 :  Porzellangefäßen 2. Wahl
A : Ausschuss

a)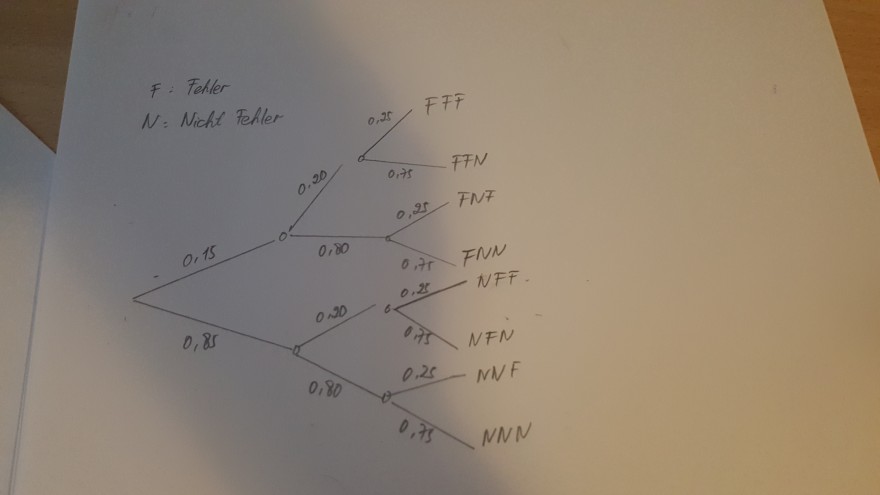  

b) P(E1) = 0,85*0,80*0,75 = 0,51 = 51 %

c) P(E2) = 0,15*0,8*0,75 + 0,20*0,85*0,75 + 0,25*0,85*0,80 = 0,3875 = 38,75 %

d) P(A) = 1 - ( P(E1) + P(E2) ) = 1 - ( 0,51+0,3875) = 0,1025 = 10,25 %

Comments

hey.

wie kommst du auf die 85 und 15

Answer 2

b) Kein Mangel: 0,85*0,8*0,75

c) 0,15*0,8*0,85+0,85*0,2+0,75+0,85*0,8*0,2

d) P(X>=2) = 1-P(X=0)-P(X=1) = 1- P(b+c)

Subtrahiere von 1 die Summe aus b) und c)