Zeigen, dass eine Funktion umkehrbar ist

Question

Aufgabe:

Text erkannt:

\( f^{\prime}(x)=\frac{-2}{(x-3)^{2}} \)

Problem/Ansatz:

Woher soll ich an der Ableitung der Funktion erkennen, dass die Funktion umkehrbar ist?!

:)

Answer 1

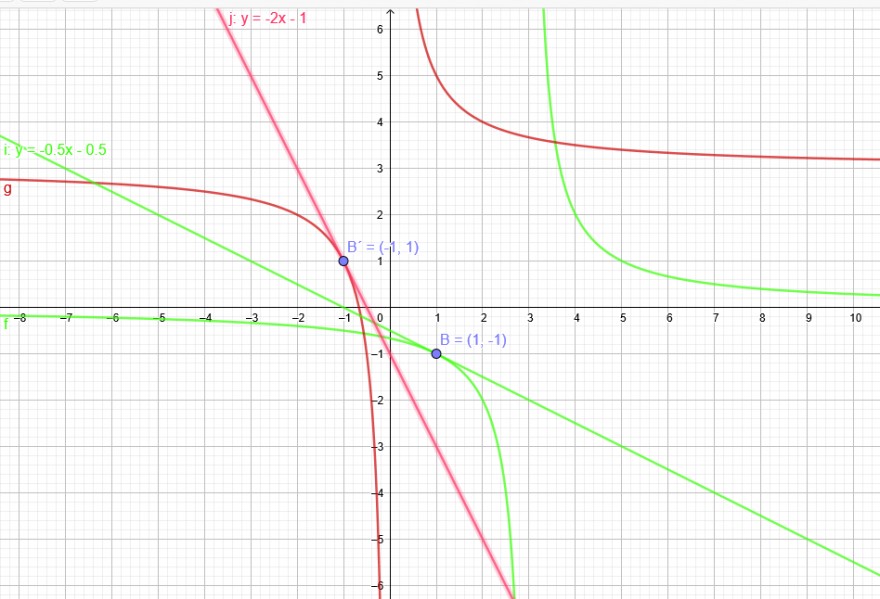
y= \( \frac{2}{x-3} \)   →  y´= - \( \frac{2}{(x-3)^2} \)   →  y´(1) = - \( \frac{2}{(1-3)^2} \) = -\( \frac{1}{2} \) in grün gezeichnet.

Umkehrfunktion:

x= \( \frac{2}{y} \)+3

x,y Tausch

y= \( \frac{2}{x} \)+3 →  y´= - \( \frac{2}{x^2} \)  →  y´(-1) = - 2  in rot gezeichnet.

Die Steigung im Punkte B(1|-1)  von y= \( \frac{2}{x-3} \)  beträgt m= -\( \frac{1}{2} \)

Die Steigung im Punkte B´(-1|1)  von y= \( \frac{2}{x} \)+3 beträgt m´= -2

Für Punkte auf y= \( \frac{2}{x-3} \)gilt nun die Steigung m

Für entsprechende Punkte auf y= \( \frac{2}{x} \)+3 gilt nun die Steigung \( \frac{1}{m} \).