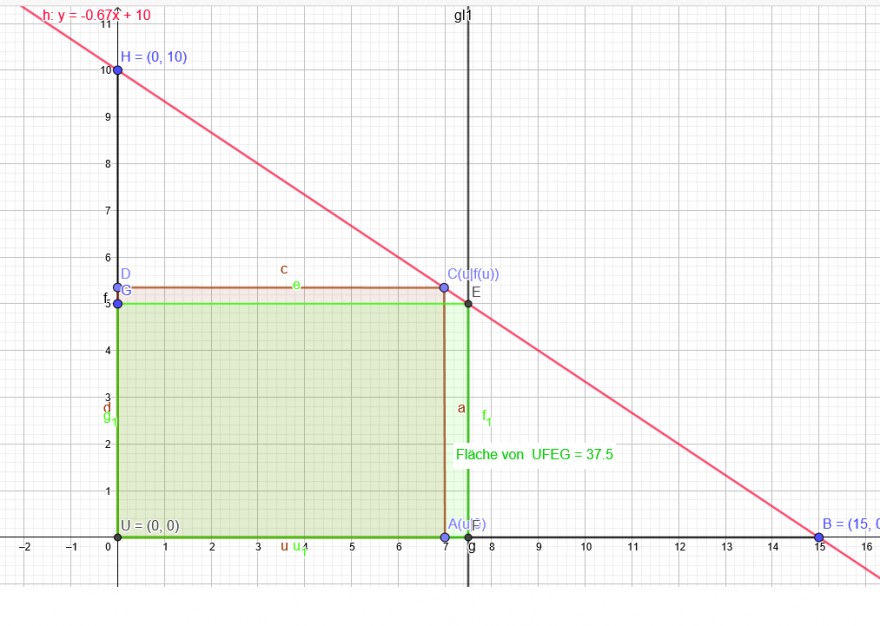
f(x)=-\( \frac{10}{15} \)x+10=-\( \frac{2}{3} \)x+10
HB: A(u)=u*f(u) soll maximal werden.
NB: f(u)=-\( \frac{2}{3} \)u+10
A(u)=u*(-\( \frac{2}{3} \)u+10) = -\( \frac{2}{3} \) \( u^{2} \)+10u
\( \frac{dA(u)}{du} \) = -\( \frac{4}{3} \) u+10
-\( \frac{4}{3} \) u+10=0
u=\( \frac{15}{2} \) =7,5
f(7,5)=-\( \frac{2}{3} \)*7,5+10=5
Die maximale Fläche beträgt 7,5*5\( m^{2} \) = 37,5\( m^{2} \)