\(V_Z=r^2\cdot π \cdot h\)
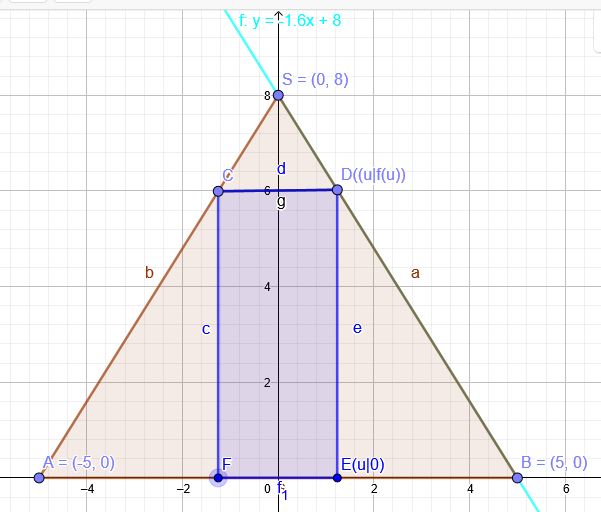
\(V(u)=u^2\cdot π \cdot f(u)\) soll maximal werden.
\(f(u)=-1,6u+8\)
\(V(u)=u^2\cdot π \cdot (-1,6u+8)\)
\(V(u)= π \cdot (-1,6u^3+8u^2)\)
\(V'(u)= π \cdot (-4,8u^2+16u)\)
\( π \cdot (-4,8u^2+16u)=0\)
\( u_1=0\) kommt nicht in Betracht
\(-4,8u+16=0\)
\(u=\frac{10}{3}\)
\(f(\frac{10}{3})=...\)