Schau dir mal die Normalparabel f(x)=x^2 an.
f(-2) =(-2) ^2=4 f(2) =(2) ^2=4
f(-1) =(-1) ^2=1 f(2) =(1) ^2=1
f(0) =(0) ^2=0 f(0) =(0) ^2=0
f(1) =(1) ^2=1
f(2) =(2) ^2=4
Bei der Normalparabel f(x)=x^2 liegt der Scheitel bei S(0|0) Nun kommt bei x=-3 und bei x=3 der gleiche Funktionswert 9 heraus. Der Scheitelpunkt S_x liegt somit in der Mitte zwischen \( \frac{-3+(+3)}{2} \)=0 S_x=0
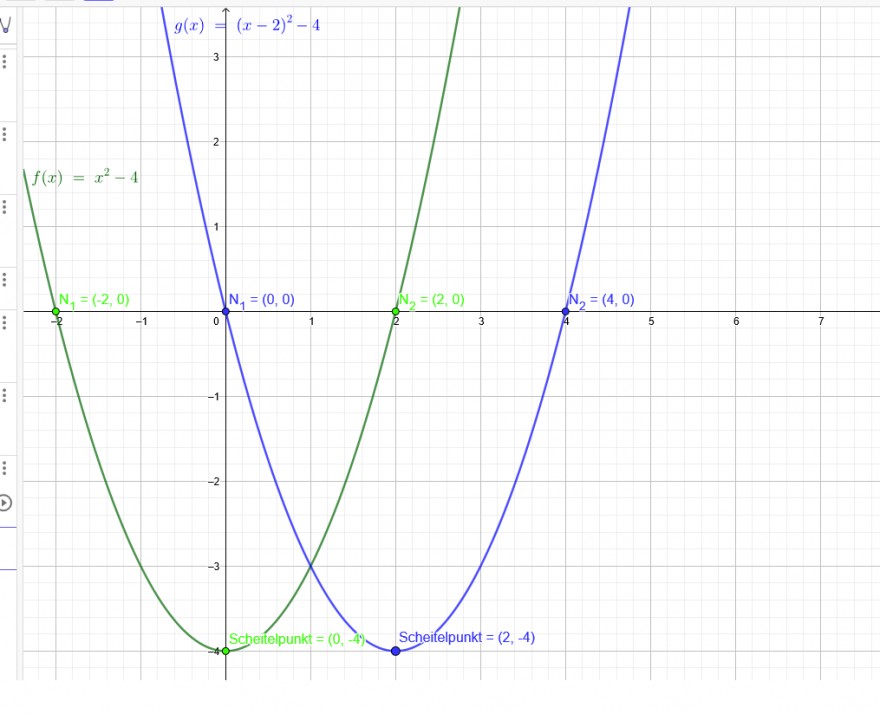
Hast du nun f(x)= x^2-4 Hier sind die beiden Nullstellen x₁=-2 und x₂=2
Dies ist nun eine um 4 Einheiten nach unten verschobene Normalparabel:
S_x = \( \frac{-2+(+2)}{2} \)=0
Verschiebst du nun f(x)=x^2-4 um 2 Einheiten nach rechts so entsteht die Parabel g(x)=(x-2)^2-4 Mit den Nullstellen x₁=0 und x₂=4 S_x = \( \frac{0+(+4)}{2} \)=2
g(2)=(2-2)^2-4=-4
Wiederum liegt der Scheitel S(2|-4 ) in der Mitte zwischen den Nullstellen.
g(x)=(x-2)^2-4=x^2-4x+4-4=x^2-4x Dies ist nun in der allgemeinen Form y=a*x^2+bx mit a=1 und b=-4 geschrieben. Nun war ja nachzuweisen, dass die Parabel hat ihren Scheitelpunkt stets an der Stelle x =- \( \frac{b}{2a} \) hat:
x=- \( \frac{-4}{2*1} \)=2
Text erkannt:
Wh