Wie lautet die Funktionsgleichung f(x) dritten Grades?

Question

Aufgabe:

Die Funktion f(x) hat den Wendepunkt W(0/-4) und einen Hochpunkt H(2/0)

Wie lautet die Funktionsgleichung f(x) dritten Grades?
Wie sieht die Skizze des Graphen der Funktion f´(x) aus?

Eine zu x-Achse parallele Gerade verläuft durch den Wendepunkt W. Wie wäre der Ansatz, wie man den Flächeninhalt zwischen beiden Graphen auf dem Intervall [0;2] berechnen kann?

Answer 1

Ansatz f(x) = ax^3 + bx^2 + xc + d

Wendepunkt  f ' ' (0) = 0

W(0/-4)              f(0) = -4

und einen Hochpunkt  f ' (2) = 0

H(2/0)               f(2) = 0 

Damit a,b,c,d bestimmen.

Answer 2

zur Kontrolle

f := -0.25*x^3 + 3*x - 4

Du rechnest die Fläche zwischen 0 und 2 aus.
Wendepunkt x = 0 , f ( 0 ) = -4
Rechteckfläche 4 * 2
Dann 4 * 2 minus die Integralfläche

Answer 3

W(0|-4) bedeutet d=-4

f''(-4)=0 bedeutet (1) 0=-24a+2b

H(2|0) bedeutet   (2) 8a+4b+2c-4=0

f '(2) bedeutet      (3) 12a+4b+c=0

Löse das System (1),(2),(3) und setze die Lösungen in f(x)=ax³+bx²+cx-4 ein.

Eine zu x-Achse parallele Gerade verläuft durch den Wendepunkt W hat die Gleichung y=-4.

Flächeninhalt zwischen beiden Graphen auf dem Intervall [0;2] \( \int\limits_{0}^{2} \) (f(x)+4) dx.

Answer 4

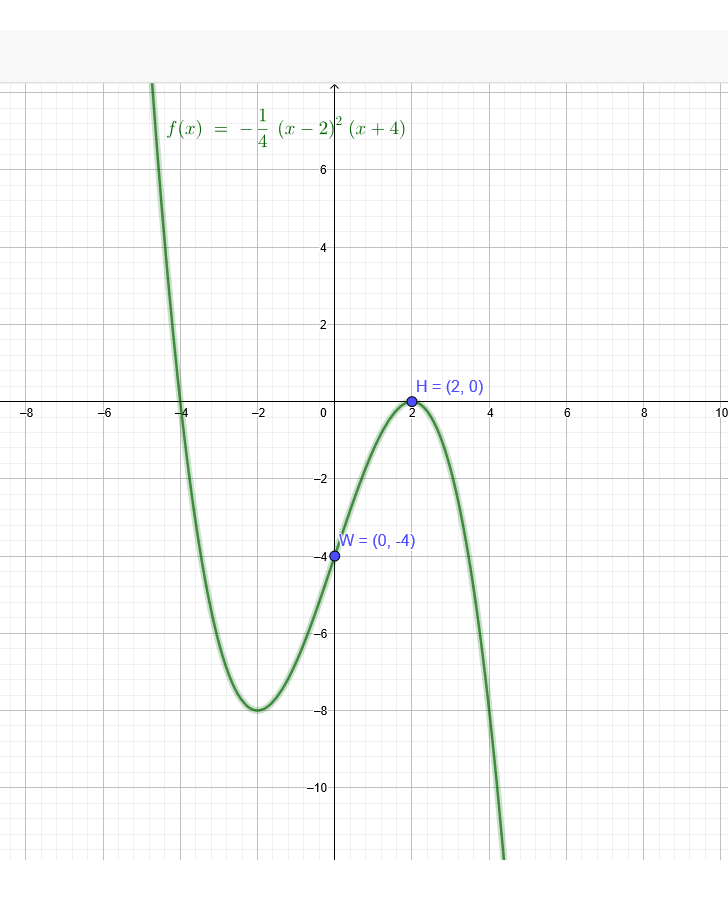
Die Funktion f(x) hat den Wendepunkt W(0|-4) und einen Hochpunkt H(2|0) 

Nullstellenform der Parabel 3.Grades

Hochpunkt H(2|0)

f(x)=a*(x-2)^2(x-N)

W(0|-4)

f(x)=a*(0-2)^2(0-N)=-4a*N

-4a*N=-4

a=\( \frac{1}{N} \)

f(x)=\( \frac{1}{N} \)*[(x-2)^2(x-N)]

f´(x)=\( \frac{1}{N} \)*[2*(x-2)*(x-N)+(x-2)^2]=\( \frac{1}{N} \)*[(2*x-4)*(x-N)+(x-2)^2]

f´´(x)=\( \frac{1}{N} \)*[2*(x-N)+(2*x-4)+2*(x-2)]

Wendepunkt(0|-4)

f´´(0)=\( \frac{1}{N} \)*[2*(0-N)+(2*0-4)+2*(0-2)]

\( \frac{1}{N} \)*[-2N-8]=0

[-2N-8]=0

N = - 4

a=-\( \frac{1}{4} \)

f(x)=-\( \frac{1}{4} \)*(x-2)^2(x+4)

Text erkannt:

W