Hallo,
Eine Linearkombination von \(a\) und \(b\) ist
$$ax + by \quad \text{mit }\space x,y \in \mathbb R$$
und wenn man irgendein Paar \(x,y\) findet, für das dieser Ausdruck \(=v\) ist, dann lässt sich \(v\) eben als Linearkombination dieser beiden Vektoren schreiben.
man könnte die Aufgabe mit einem linearen Gleichungssystem lösen,
Ja - das allgemeine Vorgehen besteht darin, für zwei der drei Koordinaten diese Gleichung zu lösen. Also
$$\begin{aligned} 3x + 0y &= 11 \\1x + 7y &= 8\\ \implies x &= \frac {11}3, \quad y = \frac{13}{21}\end{aligned}$$
Diese Parameter setzt man nun in die dritte Gleichung ein und prüft, ob sie aufgeht:
$$2 \cdot \frac{11}3 - 2 \cdot \frac{13}{21} = \frac{128}{21} \ne -3$$
D.h. \(v\) lässt sich NICHT als Linearkombination von \(a\) und \(b\) schreiben.
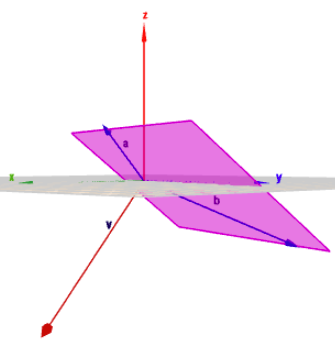
in der graphischen Darstellung sieht man ebenfalls deutlich, dass \(v\) außerhalb der Ebene liegt, die von \(a\) und \(b\) aufgespannt wird. Damit ist \(v\) nicht als Linearkombination von \(a\) und \(b\) darstellbar.