Berechnen Sie die Größe des Winkels, den die Dachfläche SFG mit der Grundfläche der Pyramide einschließt!

Question

Aufgabe:

Aufgabe 2: Als Besucherplattform für die Beobachtung der Nachstellung der Schlacht von Jena und Auerstedt wird ein Holzturm auf einer ebenen Fläche errichtet. Er besteht aus einem Quader mit aufgesetzter gerader Pyramide. Die Koordinaten folgender Punkte seien gegeben: A(9|0|0), B(9|12|0); C(0|12|0) und E(9|0|20). Eine Einheit im Koordinatensystem betrage einen Meter in der Realität. Die Höhe der Pyramide betrage fünf Meter.
a) Berechnen Sie die Größe des Winkels, den die Dachfläche SFG mit der Grundfläche der Pyramide einschließt!
b) Die Gerade g durch die Dachkante SF und die Gerade h durch die Diagonale EG verlaufen windschief zueinander. Berechnen Sie den Abstand beider Geraden!
c) Auf der Spitze der Pyramide stehe eine 3m hohe Antenne. Die Richtung des
Sonnenlichtes werde durch den Vektor beschrieben. Untersuchen Sie, ob der
Schatten der Antenne vollständig in der Dachfläche SFG liegt!

Problem/Ansatz:

Hallo liebe Leute, leider war ich in Mathe nie gut in Geometrie. Kann mir einer helfen diese Aufgaben zu lösen ?? Wäre wirklich sehr hilfreich

Answer 1

Hallo,

a) Berechnen Sie die Größe des Winkels, den die Dachfläche SFG mit der Grundfläche der Pyramide einschließt!

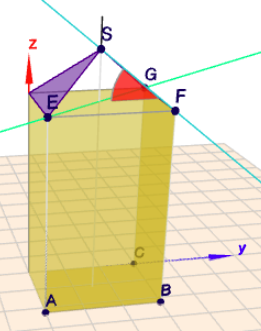
Denke Dir einen senkrechten Schnitt durch die Pyramide, parallel zur yz-Ebene, der den Punkt \(S\) enthält. Ist der gesuchte Winkel \(\varphi\) (rot), so ist$$\tan \varphi = \frac{h_P}{\frac 12 |AB|} = \frac 56 \implies \varphi \approx 39,81°$$

b) Die Gerade g durch die Dachkante SF und die Gerade h durch die Diagonale EG verlaufen windschief zueinander. Berechnen Sie den Abstand beider Geraden!

Berechne zunächst den Normalenvektor \(\vec n\) der Länge 1, der senkrecht auf beiden Geraden steht:$$\vec{FS} \times \vec{EG} = \begin{pmatrix}4.5\\ 6\\ -5\end{pmatrix} \times \begin{pmatrix}-9\\ 12\\ 0\end{pmatrix} = \begin{pmatrix}60\\ 45\\ 108\end{pmatrix} \\ \implies \vec n = \frac 1{\sqrt{}1921} \begin{pmatrix}20\\ 15\\ 36\end{pmatrix}$$Der Abstand \(d\) der beiden Geraden ist dann die Differenz der Skalarprodukte zweier Punkte der Geraden mit \(\vec n\)$$d = |E \cdot \vec n - S \cdot \vec n| = |(E-S) \cdot \vec n| \\ = \left|\begin{pmatrix}4.5\\ -6\\ -5\end{pmatrix} \cdot \frac 1{\sqrt{}1921} \begin{pmatrix}20\\ 15\\ 36\end{pmatrix} \right| = \frac{180}{\sqrt{1921}} \approx 4,11$$

c) Auf der Spitze der Pyramide stehe eine 3m hohe Antenne. Die Richtung des Sonnenlichtes werde durch den Vektor beschrieben.

Da fehlt noch 'der Vektor' in Deiner Aufgabenstellung.