h(x)=3e^(-1/3x+3)-3
a) Ermitteln Sie rechnerisch die Nullstellen der Funktion h:
Deine Nullstelle ist richtig.
b) Berechnen Sie x so, dass die Tangente t an den Graphen G den Anstieg m=–2/3 hat
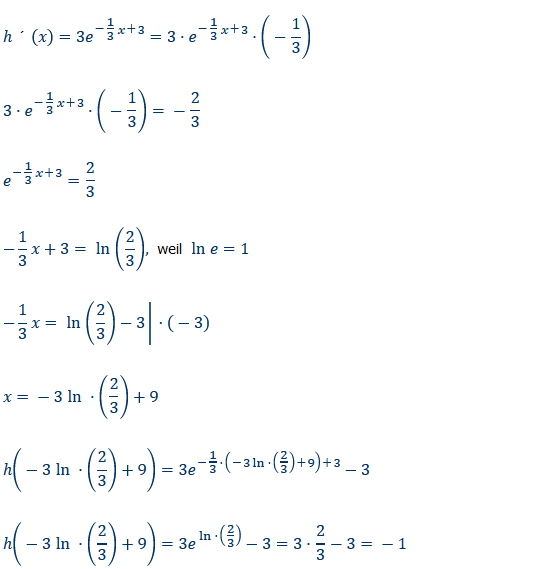
Text erkannt:
\( h^{\prime}(x)=3 e^{-\frac{1}{3} x+3}=3 \cdot e^{-\frac{1}{3} x+3} \cdot\left(-\frac{1}{3}\right) \)
\( 3 \cdot e^{-\frac{1}{3} x+3} \cdot\left(-\frac{1}{3}\right)=-\frac{2}{3} \)
\( e^{-\frac{1}{3} x+3}=\frac{2}{3} \)
\( -\frac{1}{3} x+3=\ln \left(\frac{2}{3}\right), \) weil \( \ln e=1 \)
\( -\frac{1}{3} x=\ln \left(\frac{2}{3}\right)-3 \mid \cdot(-3) \)
\( h\left(-3 \ln \cdot\left(\frac{2}{3}\right)+9\right)=3 e^{-\frac{1}{3} \cdot\left(-3 \ln \cdot\left(\frac{2}{3}\right)+9\right)+3}-3 \)
\( x=-3 \ln \cdot\left(\frac{2}{3}\right)+9 \)
\( \left(-3 \ln \cdot\left(\frac{2}{3}\right)+9\right)=3 e^{\ln \cdot\left(\frac{2}{3}\right)}-3=3 \cdot \frac{2}{3}-3=-1 \)
c) Der Graph G begrenzt mit den Koordinatenachsen eine Fläche vollständig. Ermitteln Sie diese Fläche

Text erkannt:
\( A=\int \limits_{0}^{9}\left(3 e^{-\frac{1}{3} x+3}-3\right) \cdot d x=3 \cdot \int \limits_{0}^{9}\left(e^{3-\frac{1}{3} x}\right) \cdot d x-3 \int \limits_{0}^{9} d x= \)
\( =3 e^{3} \cdot \int \limits_{0}^{9} e^{-\frac{1}{3} x} \cdot d x-3 \cdot \int \limits_{0}^{9} d x \)
Substitution:
\( \int e^{-\frac{1}{3} x} \cdot d x=\int e^{u} \cdot(-3) \cdot d u=-3 \int e^{u} \cdot d u \)
\( -\frac{1}{3} x=u \rightarrow \rightarrow-\frac{1}{3} x=u \)
\( x=-3 u \)
\( d x=-3 \cdot d u \)
\( \int e^{-\frac{1}{3} x} \cdot d x=\int e^{u} \cdot(-3) \cdot d u=-3 \int e^{u} \cdot d u=-3 e^{u} \)
Und zurück:
\( \int e^{-\frac{1}{3} x} \cdot d x=-3 \cdot e^{-\frac{1}{3} x} \)
\( u \cdot S \cdot W \)