maximieren: A( Dreieck)= 0,5×(f(x)×(6-x)?

Question

Aufgabe: Gegeben ist die Parabel f(x)=-0,25x^2+x+3    a) Berechnen Sie die Nullstellen und den Scheitelpunkt der Parabel. b) Auf der Parabel liegt der Punkt P. Dieser bildet zusammen mit dem y-Achsendurchgang, koordinatenursprung und der rechten Nullstelle ein Fünfeck. ( Trapez und Dreieck)  x muss größer als 0 sein. Ermitteln Sie Punkt P so, dass das Fünfeck den größen Flächeninhalt hat.

Problem/Ansatz: maximieren: A( Dreieck)= 0,5×(f(x)×(6-x) ??? weiter komm ich nicht und P ist nicht am größten wenn man automatisch den Scheitelpunkt einsetzt? S(2/4) rechte NS(6/0)

Answer 1

Hallo

bild : 2 mögliche Vierecke (kein Fünfeck.) mit den 2 Punkten   F oder C, mit F Scheitel., kein Grund das das das größte Viereck din sollte, also nenn die x- Koordinate   z.B, a, dann hast du das Trapez mit den parallelen Seiten  3 und f(a) und das Dreieck mit den Katheten (6-a) und f(a)

bestimme  die 2 Flächen und addiere sie zu A(a) dann suche das max davon  du nennst a x, dann ist die Fläche des Dreiecks richtig (vermeide bitte Malzeichen, die wie x aussehen)

Gruß lul

Comments

Ich hab das jetzt so geschrieben A(Dreieck)=((6-x)× f(x))×0,5    A(Trapez)=(3+f(x))÷2×x  und für x setze ich 2 und für f(x) 4 ein? Der SP ist HP der Parabel, denn suche ich aber nicht sondern eine Funktion oder?

---

Hallo

ja du suchst die Funktion A(x) das ist die Summe der 2 A die du richtig ausgerechnet hast (obwohl trotz meiner Bitte wieder die x- malzeichen)

davon suchst du dann das Max. d,h, du leitest A(x) ab und suchst die Nullstelle.

lul

Answer 2

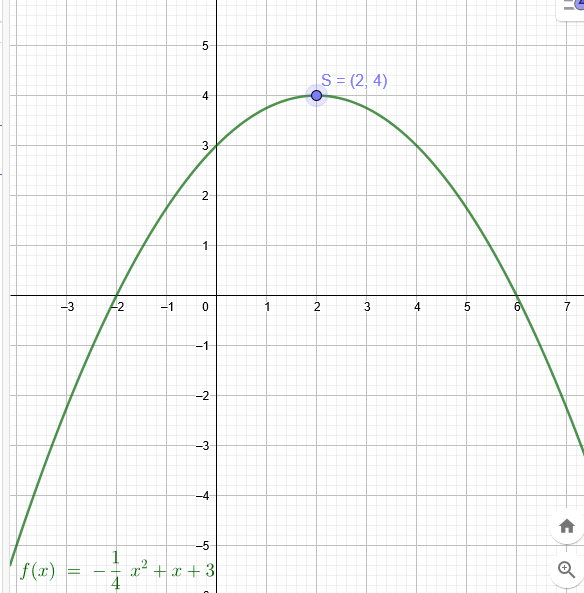
Aufgabe: Gegeben ist die Parabel f(x)=-0,25x^2+x+3

a) Berechnen Sie die Nullstellen und den Scheitelpunkt der Parabel

Nullstellen:  -0,25x^2+x+3 =0 |*(-4)

x^2-4x =12

(x-2)^2=12+4=16 | \( \sqrt{} \)

1.) x-2=4

x₁=6

1.) x-2=-4

x₂=-2

Scheitelpunkt:

Bei einer Parabel 2. Grades liegt der x - Wert immer in der Mitte zwischen den Nullstellen:

x_S= \( \frac{6+(-2)}{2} \)=2

f(2)=-0,25*4+2+3 =4

S(2|4)