Wie lautet die Gleichung von N? Wie viele Einwohner gewinnt die Stadt in dem 20-Jahres-Zeitraum hinzu?

Question

Aufgabe:

Eine Stadt hat zu Beginn eines Planungszeitraumes 2 mio. Einwohner. Ein Institut geht davon aus, dass die Änderungsrate der Einwohnerzahl N in den nächsten 20 Jahren durch die lineare Funktion N'(t)=0,002x + 0,05 modelliert werden kann. Wie lautet die Gleichung von N? Wie viele Einwohner gewinnt die Stadt in dem 20 - Jahres - Zeitraum hinzu?

Problem/Ansatz:

Ich sitze schon nun sehr lange an dieser Aufgabe und überlege hin und her. Ich komme einfach nicht auf die Lösung geschweige denn finde ich einen Ansatz für diese Aufgabe.

Ich hoffe mir kann jemand helfen lg :)

Answer 1

1.Ableitung
N' ( t ) = 0,002x + 0,05
Funktion
int ( N´) zwischen 0 und x
N ( t ) = 0.002 * x^2 / 2 + 0.05x
N ( t ) = 0.001 * x^2  + 0.05x
N ( 20 ) = 0.001 * 20^2 + 0.05 * 20
N ( 20 ) = 1.4 MIo
1.4 Mio Zuwachs

C = 2 Mio
Gesamtpopulation 1.4 + 2

Schon die Aufgabenstellung stimmt nicht
anstelle
N' ( t ) = 0,002x + 0,05
muß es heißen
N' ( x ) = 0,002x + 0,05
oder
N' ( t ) = 0,002t + 0,05

Comments

Dankeschön✌️

---

Gern geschehen.

---

Kann mir vielleicht noch jemand den Rechenweg erklären? :) lg

---

Ich erkläre dir das Ganze einmal
ohne Differentlialrechnung

Ich erkläre einmal mit der
Analogie zu Weg und Geschwindigkeit

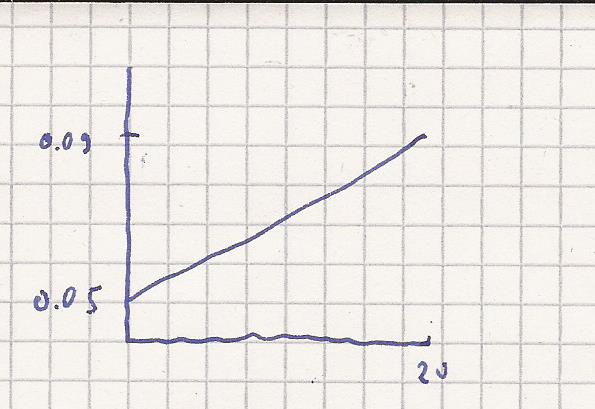
Dies könnte auch eine Geschwindigkeitfunktion
sein. Erste Ableitung einer Wegfunktion.

v ( x ) = 0.002 * x + 0.05

v ( 20 ) = 20 * 0.002 + 0.05 = 0.09 m/s

v ( mittel ) = ( 0.05 + 0.09 ) / 2 = 0.07 m/s
Der Weg
s = v ( mittel ) * t = 0.07 * 20 = 1.4 m

Derselbe Rechenweg gilt auch für die
Zunahme der Bevölkerung.

N´( x ) = 0.002 * x + 0.05
N´ ( 20 ) = 20 * 0.002 + 0.05  = 0.09
N´ ( mittel ) = ( 0.05 + 0.09 ) / 2 = 0.07
Bevölkerung
N = N´ ( mittel ) * t = 0.07 * 20 = 1.4 MIo

Frag nach bis alle Klarheiten beseitigt sind.

Du sollst nicht unwissend sterben.

---

Vielen lieben Dank für die erstklassige Hilfe! Wirklich. Ich denke, dass ich es jetzt soweit verstanden habe.

---

Schön. Fülltext.

Answer 2

Rate in Einw. / Jahr oder Mio Einwohner pro Jahr . wohl das zweite ???

N'(t)=0,002x + 0,05   ==>   N(t) = 0,001x^2 + 0,05x + C

(Stammfunktion suchen .)

Wegen N(0) =  C ist C = 2 Mio.

Nach 20 Jahren also N(t) = 0,001*400 + 0,05*20+ 2 = 0,4+1+2 = 3,4 Mio

Also 1,4 Mio Zuwachs.

Comments

Vielen lieben Dank für die schnelle Rückmeldung. Könnte das eventuell auch jemand für mich erklären? :)

---

Wenn du die Änderungsrate einer Funktion hast, dann ist

die Funktion selber immer eine Stammfunktion dazu,

also eine, deren Ableitung die Änderungsrate ergibt.