Trigonometrie Behauptıngen Beweisen

Question

Text erkannt:

12 Beweisen \( \alpha \) und \( \beta \) sind die beiden spitzen Winkel eines rechtwinkligen Dreiecks. Beweise, dass dann die folgenden Behauptungen richtig sind.
a) \( \sin (\alpha)=\cos (\beta) \)
b) Die Werte von \( \cos (\alpha) \) und von \( \sin (\alpha) \) sind stets kleiner als 1.
c) Die Werte von \( \tan (\alpha) \) können beliebig groß werden.
d) Ist das Dreieck gleichschenklig, so gilt \( \sin (\alpha)=\cos (\alpha) \) und \( \tan (\beta)=\tan (\alpha)=1 \).

Answer 1

a)

sin(α)=\( \frac{a}{c} \)=cos(β).

b) Sowohl α<90° als auch β<90°.

c) Die Gegenkathete b von β kann beliebig lang werden und die Ankathete a kann unverändert bleiben. tan(β)=\( \frac{b}{a} \).

d) Hier ist sogar α=β:

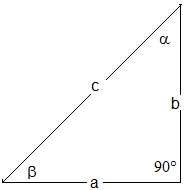
und für a=b ist \( \frac{a}{b} \)=\( \frac{b}{a} \)=1