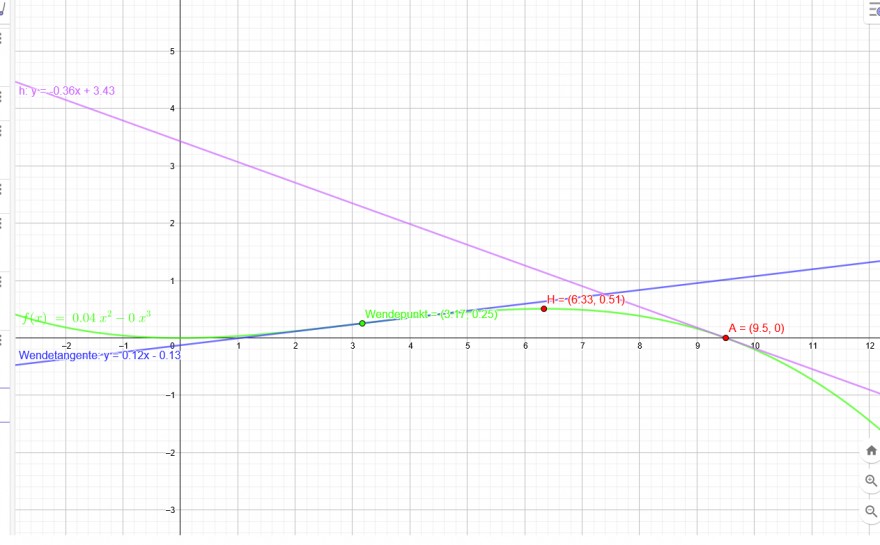
f(x)=0,038x^2−0,004x^3
1) Welche Querschnittslänge hat der Berg? → f(x)=0
0,038x^2−0,004x^3=0
x^2*(0,038-0,004x)=0
x_1,2=0 doppelte Nullstelle Extremwert
0,038-0,004x=0 x≈9,5 Querschnittlänge ≈9,5km
2) Wie hoch ist der Berg? → f´(x)=0
f´(x)=0,076x−0,012x^2
0,076x−0,012x^2=0
x*(0,076-0,012x)=0
x_1=0 f(0)=0 siehe auch unter 1)
0,076-0,012x=0
x_2 ≈6,33333 f(6,33333)=0,038*6,33333^2−0,004*6,33333^3≈0,508
Der Berg ist ungefähr 508m hoch.
3a) Wie groß ist der Anstieg maximal, wenn der Wanderer von Westen kommt?
f´´(x)=0,076−0,024x
0,076−0,024x=0 x≈3,17 f´(3,17)=0,076*3,17−0,012*3,17^2≈0,12 tan^-1(0,12)≈6,8° entspricht 11,92%
3b) Wie groß ist der Anstieg maximal, wenn der Wanderer von Osten kommt?
Am Anfang des Berges bei x=9,5 beträgt die Steigung f´(9,5)=0,076*9,5−0,012*9,5^2=-0,361 tan^-1(-0,361 )=|-19,85°|=19,85° entspricht 36,1%