Berechnen Sie zu welchem Zeitpunkt

Question

Text erkannt:

Aufgabe \( 2_{i}(17 \mathrm{BE}) \)
Der Temperaturverlauf eines Tages auBerhalb eines Hauses kann durch den Graphen einer Funktion \( f \) mit \( f(t)=-\frac{1}{90} t^{3}+\frac{1}{3} t^{2}-\frac{8}{5} t+15 \) fur \( t \in[0 ; 24] \) beschrieben werden. Die
nebenstehende Abbildung zeigt den
Graphen der Funktion \( f . \) Dabei ist \( t \) die
Zeit in Stunden und \( f(t) \) die
AuBentemperatur in \( { }^{\circ} \mathrm{C} \)
a) Beschreiben Sie anhand der
graphischen Darstellung mit eigenen
Worten den Verlauf des Graphen im
Sachzusammenhang.
b) Berechnen Sie zu welchem Zeitpunkt
die Temperatur minimal bzw. maximal
wird.
Berechnen Sie die Temperaturschwankung (Unterschied zwischen Temperaturmaximum und
-minimum an diesem Tag).
c) Bestimmen Sie die Zeitspanne, in der es kalter als um 0.00 Uhr ist.
d) Berechnen Sie den Zeitpunkt des stairksten Temperaturanstiegs und geben Sie den
Temperaturanstieg zu diesem Zeitpunkt an.
Aufgabe \( 3:(10 \mathrm{BE}) \)
Ein Bauer will eine rechteckige Grünfliche einziunen. Dafur stehen ihm 40 Meter Zaun zur
Verfugung. Eine 2 Meter breite Einfahrt soll dabei berücksichtigt werden.

Bestimmen Sie die Länge der Seitenlängen der Grünflaiche, wenn diese möglichst groB sein
soll. Fertigen Sie zuerst eine Skizze an.
Aufgabe \( 4:(10 \mathrm{BE}) \)
Der zur y-Achse symmetrische Graph einer ganzrationalen Funktion 4. Grades geht durch
\( \mathrm{P}(0 \mid 2) \) und hat bei \( \mathrm{x}=2 \) ein Extremum. Er berührt dort die \( \mathrm{x} \) - Achse.
Bestimmen Sie die Gleichung der Funktion \( f \) mit den beschriebenen Eigenschaften.

Ich brauche Hilfe bei meinen Übungsaufgaben!

Answer 1

a) Nach 0.00 Uhr sinkt die Temperatur bis ca. 2.15 Uhr danach steigt sie bis ca. 16.30 Uhr und sinkt dann wieder. auf den Ausgangswert.

Answer 2

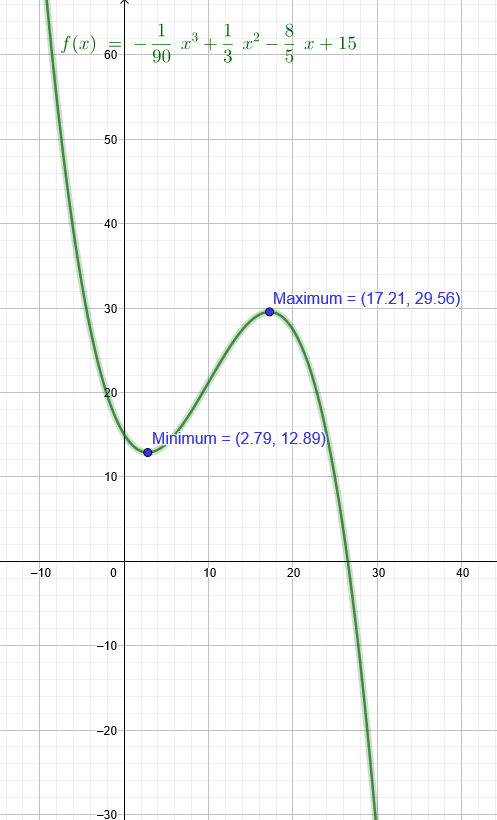
b) Berechnen Sie zu welchem Zeitpunkt die Temperatur minimal bzw. maximal wird.

f(t) = − \( \frac{1}{90} \) \( t^{3} \)+\( \frac{1}{3} \) \( t^{2} \)-\( \frac{8}{5} \)t+15

Extremwertbestimmung:   f´(t) =0

f´(t) = − \( \frac{1}{30} \) \( t^{2} \)+\( \frac{2}{3} \) t-\( \frac{8}{5} \)

− \( \frac{1}{30} \) \( t^{2} \)+\( \frac{2}{3} \) t-\( \frac{8}{5} \)=0|*(-30)

 \( t^{2} \)-20t = - 48

(t-10)^2=52|\( \sqrt{} \)

t₁=10+\( \sqrt{52} \)    noch in Uhrzeit umrechnen

t₂=10-\( \sqrt{52} \)      noch in Uhrzeit umrechnen

Art des Extremwertes:

f´´(t) = − \( \frac{1}{15} \) *t+\( \frac{2}{3} \) 

f´´(t) = − \( \frac{1}{15} \) *t+\( \frac{2}{3} \)

f´´(t₁) = − \( \frac{1}{15} \) *(10+\( \sqrt{52} \))+\( \frac{2}{3} \) ≈ - 0,5 < 0    Maximum

f´´(t₁) = − \( \frac{1}{15} \) *(10-\( \sqrt{52} \))+\( \frac{2}{3} \) ≈  0,5 >0    Minimum

Answer 3

c)

f(0)=15. Um 0 Uhr liegt die Außentemperatur also bei 15°C.

Bed.: f(t)=15 ⇔ −\( \frac{1}{90} \)t³+\( \frac{1}{3} \)t²−\( \frac{8}{5} \)t+15=15 ⇒ t=0 v t=6 v t=24, d.h. um 0 Uhr, um 6 Uhr und um 24 Uhr lag die Außentemperatur bei 15°C.

Jetzt musst du dir nur noch den Graphen anschauen und dir sollte schnell auffallen, dass es für 0<t<6 kälter als um 0 Uhr war.

Also: nach 0 Uhr bis vor 6 Uhr war es also kälter als um 0 Uhr.

d) ges. ist der abs. Hochpunkt von f'

notw. Bed.: f''(t)=0

hinr. Bed.: f''(t)=0 ∧ f'''(t)≠0

Temperaturanstieg zu diesem Zeitpunkt: f'(x₀)=...