Ein Kind im Vorschulalter ist in der Lage, fünf Fingern seiner Hand, fünf Kerzen auf dem Geburtstagskuchen und den fünf Personen am Geburtstagskaffeetisch ein gemeinsames Merkmal anzusehen. Ob es dieses gemeinsame Merkmal mit dem Wort ‚fünf‘ auch benennen kann, hängt davon ab, wie weit das mechanische Nachplappern der Wortfolge „eins, zwei, drei, vier, fünf, …“ bereits zum Zählen verwendet werden kann. Unabhängig von dieser Benennung ist bereits das Erkennen der Gemeinsamkeit (von Mathematikern auch ‚Mächtigkeit‘ genannt) der genannten ‚Fünfheiten‘ eine vom Kind erbrachte Abstraktionsleistung. Die semiotische Konkretisierung der Abstraktion durch ein Wort oder durch ein Zahlzeichen ermöglicht nicht nur die Mitteilung der entdeckten Gemeinsamkeit an Dritte, sondern erleichtert dem Kind auch den Einbau in weiterführende Gedanken, wie zum Beispiel in die Addition von Mächtigkeiten.
Eine wiederholte Addition gleicher Mächtigkeiten, wie zum Beispiel die Addition von sechs Fünfen, wird sprachlich als „sechs mal fünf“ zum Ausdruck gebracht. Das Wort ‚mal‘ impliziert die Verknüpfung zweier Mächtigkeiten zu einer neuen Mächtigkeit. Und das Wort ‚mal‘ wird durch ein Zeichen ‚·‘ stenographiert, was den Einbau in einen weiterführenden Gedanken erleichtert. Nach Peirce sind die Zeichen die Grundelemente des Denkens; „There is no thinking without signs“. Allerdings ist für Peirce bereits das Wort ‚fünf‘ ein Zeichen. In diesem Sinne kann allein die Abstraktion aus verschiedenen Mengen gleicher Mächtigkeit im Gehirn des Kindes als ein Zeichen aufgefasst werden, auch wenn eine Kommunikation über dieses Zeichen – Mangels Begriff – noch unmöglich ist. Auch der Einbau eines Zeichens ohne begriffliche Konkretisierung (Wort, Bild oder Symbol) in einen weiterführenden Gedanken dürfte sehr erschwert, wenn nicht sogar unmöglich sein.
Eine Abstraktion (letztlich eine Verallgemeinerung) wird nur dann greifbar und so in einen weiterführenden Gedanken einbaubar, nachdem sie sich vergegenständlicht hat – vergegenständlicht in einem Wort, Bild oder Symbol. In diesen Wörtern, Bildern und Symbolen denken und kommunizieren wir. Peirce bezeichnet diese vergegenständlichende Verallgemeinerung als hypostatische Abstraktion. Jedes Nomen unserer Sprache ist das Ergebnis einer hypostatischen Abstraktion, mittels derer irgendwann in der Entwicklung unserer Sprache irgendetwas auf den ‚Begriff‘ gebracht wurde.
Nach Chomsky ist die ‚Fähigkeit zur Sprache‘ die Wurzel rekursiven Denkens. Dieser Zusammenhang kann (z.B. nach Peirce) ebenso gut auch umgekehrt gesehen werden: Rekursives Denken ist ein Aspekt menschlicher Kognition, aus dem heraus sich das Werkzeug ‚Sprache’ entwickelt hat. Tatsächlich geht es um die Bildung von Begriffen auf der Grundlage bereits abstrahierter Begriffe. Dabei müssen Begriffe zueinander in Beziehung gesetzt werden, also in Aussagen oder Aussageformen verarbeitet werden. Die Transformation von Aussagen und Aussageformen in gleichwertige Aussagen und Aussageformen geschieht auf der Grundlage allgemein anerkannter Regeln. Diese Regeln bilden zusammen mit den Begriffen ein ‚Darstellungssystem‘. Bekanntes Beispiel für die Regeln eines Darstellungssystems sind die Regeln der Termumformung oder die Regeln der Gleichungslehre. Die meisten Zusammenhänge können verbal, formal oder bildlich dargestellt werden. Der Wechsel zwischen den Darstellungen (Peirce nennt sie ‚Diagramme‘) unterliegt allgemein anerkannten Regeln. Ein mathematisches Problem (z.B. eine Aufgabe aus dem Lehrbuch) wird oft zunächst verbal beschrieben. Nach Umwandlung in eine formale Beschreibung lässt diese sich nach anerkannten Regeln äquivalent umformen oder als Bild darstellen.
Ein Beispiel:
Aufgabe: Zeigen Sie: Ein Quadrat mit der Seitenlänge c wird von vier rechtwinkligen Dreiecken mit der Hypotenuse c und den Katheten a und b sowie einem Quadrat mit der Seitenläge |a-b| vollständig und ohne Überschneidungen überdeckt.
Diese verbale Beschreibung eines Sachverhaltes wird zunächst formalisiert:
(1) 4·(a∙b)/2+|a-b|2=c2
Diese Gleichung wird nach den Regeln der Termumformung in eine äquivalente Gleichung transformiert:
(2) 2·a·b+a2-2ab+b2=c2
und weiter (3) a2+b2=c2.
Zeile (3) nennt nun eine bekannte Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks und ist folglich für rechtwinklige Dreiecke allgemeingültig. Damit sind auch die Zeilen (1) und (2) unter den in der Aufgabe genannten Bedingungen allgemeingültige Aussageformen. Die verbal formulierte Aufgabe ist damit gelöst.
Man kann den in der Aufgabe geschilderten Sachverhalt auch bildlich darstellen (siehe unten).
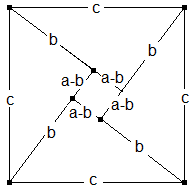
Dann ergibt sich aus der Darstellung ein anschaulicher Beweis des Satzes von Pythagoras. Der Satz von Pythagoras kann nun eingebaut werden in Lösungswege zu zahlreichen weiteren Aufgaben.
Die Rekursivität des Denkens ist auf diese Weise eine Strategie zur Problemlösung. Da die Aufgabe sprachlich formuliert war, werden wir an dieser Stelle an Chomsky erinnert, der die ‚Fähigkeit zur Sprache‘ für die ‚Wurzel des rekursiven Denkens‘ hält. Umgekehrt braucht die bildliche Übersetzung der Aufgabe nur noch die Sprache der Mathematik, um zum Satz des Pythagoras zu führen. Die Sprache der Mathematik begleitet rekursives Denken oder macht dieses überhaupt erst möglich. Die Sprache der Mathematik hat sich möglicherweise aus dem rekursiven Denken entwickelt.
