Fixpunktproblem das konvergiert finden

Question

Aufgabe:

x^3-x-1=0

Ein Nullstellenproblem sei gegeben, wandeln Sie dieses in ein Fixpunktproblem um. Erwarten Sie das diese Funktion konvergiert?

Problem/Ansatz:

Mein Problem mit diesem Beispiel ist das nicht jede Umwandlung zu einem Fixpunktproblem konvergiert. Bringe ich beispieslweise x auf die andere Seite, würde dieses Fixpunktproblem (x^3-1) nicht konvergieren. Die Funktion würde gegen minus unendlich gehen. Wenn ich aber x^3 auf die andere Seite rüberbringe haben wir dieses Fixpunktproblem( (x+1)^1/3 ) Dieses konvergiert gegen 1.325.

Meine Frage, wie forme ich mein Nullstellenproblem so um, dass dieses konvergiert? Also gleich beim Ersten Versuch, gibt es dafür eine Methode?

Answer 1

Aloha :)

Hier lautet das Stichwort "Banachscher Fixpunktsatz". Praktisch kannst du dir merken, dass \(f(x)=x\) in der betrachteten Definitionsmenge\(M\) gegen genau eine Lösung konvergiert, wenn es eine Konstante \(c<1\) gibt, sodass \(f'(x)\le c\) für alle \(x\in M\) ist. Es reicht also nicht, dass \(f'(x)<1\) ist, sondern du musst eine Konstante \(c<1\) als obere Schranke für die Ableitung angeben können.

In deinem Fall heißt das:$$x^3-x-1=0\quad\Longleftrightarrow\quad x^3=1+x\quad\stackrel{(x\ge0)}\Longleftrightarrow\quad x=\sqrt[3]{1+x}\eqqcolon f(x)$$

Wegen \(f'(x)=\frac{1}{3}(1+x)^{-2/3}=\frac{1}{3\sqrt[3]{(1+x)^2}}\) kannst du z.B. für \(x\ge0\) sicher sein, \(f'(x)\le\frac{1}{3}<1\) ist und daher genau ein Fixpunkt mit \(x\ge0\) exisitiert.

Comments

das ist mir ja alles bewusst. Ich weiß nicht, ob ich deine Antwort missverstehe oder du meine Frage. Meine Frage war, wie forme ich ein Nullpunktproblem in ein Fixpunktproblem so um das es konvergiert (falls es halt möglich ist). Ohne ausprobieren

---

Du musst \(f(x)\) so bilden, dass die Ableitung \(<1\) ist.

---

Beachte die Regel für die Ableitung der Umkehrfunktion in diesem Zusammenhang :

(f^-1)' (x)  =  1 / f'(f^-1(x))  zusammen mit der Tatsache, dass falls   a > 1  dann 1/a < 1  ist und umgekehrt.

Beispiel :

 

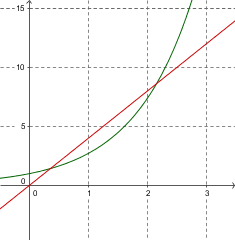
Gesucht sind Lösungen der Gleichung e^x = 4x

Die Fixpunktiteration mit der Funktion f mit f(x) = ln (4x)  [f'(x) = 1/(4x)]  konvergiert gegen 2,15.. ,

die Fixpunktiteration mit der Funktion f^-1 mit f^-1(x) = e^x/4 [(f^-1)'(x) = e^x/4] konvergiert gegen 0,357..

(jeweils bei geeignetem Startwert)

Tipp : Wenn f nicht klappt, dann versuche es mit f^-1