Aufgabe:
Beweise mit den Methoden der Vektorrechnung, dass in einem beliebigen Viereck die abwechselnde Verbindung zwischen den Mittelpunkten von zwei gegenüberliegenden Seiten und der Mittelpunkte der Diagonalen ein Parallelogramm ergibt.
Problem/Ansatz:
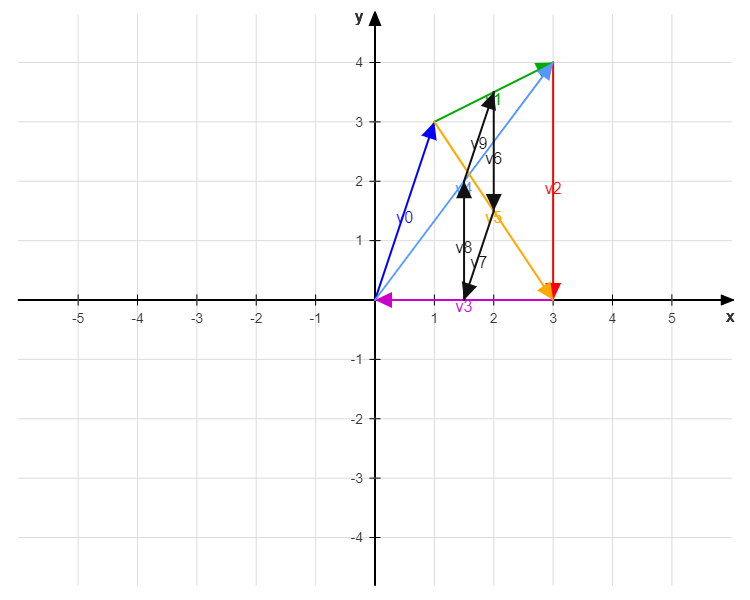
Ich steh so ein bisschen auf dem Schlauch wie ich den Beweis führen soll. Die Vektoren habe ich schon aufgestellt (s. Skizze im Anhang):
Vektoren die das Viereck bilden: $$\vec{v_{0}}, \vec{v_{1}}, \vec{v_{2}}, \vec{v_{3}}$$
Diagonalen: $$\vec{v_{4}}, \vec{v_{5}}$$
Resultierende Vektoren fürs Parallelogramm:
$$\frac{1}{2}\vec{v_{1}}-\frac{1}{2}\vec{v_{5}} = \vec{v_{6}}\\ \frac{1}{2}\vec{v_{6}}+\frac{1}{2}\vec{v_{3}} = \vec{v_{7}}\\ \frac{1}{2}\vec{v_{3}}+\frac{1}{2}\vec{v_{4}} = \vec{v_{8}}\\ \frac{1}{2}\vec{v_{4}}-\frac{1}{2}\vec{v_{1}} = \vec{v_{9}}$$
Wie zeige ich jetzt am besten das es sich um ein Parallelogramm handelt? Ich vermute mal, am ungeschicktesten wäre es ja über Parallelität und gleiche Länge zu gehen, aber hier hapert es gerade.