Aufgabe:
Zeigen Siemit vollständiger Induktion, dass für allen n∈N gilt:
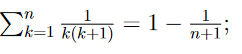
Text erkannt:
\( \sum \limits_{k=1}^{n} \frac{1}{k(k+1)}=1-\frac{1}{n+1} \)
Ergebnis: 1 - 1/n+2
Problem/Ansatz:
Im Induktionsschritt bzw. beim gleichsetzen komme ich durcheinander.
Ich komme bis zu dem Teil:
= 1 - 1/(n+1) + 1/(n+1)*(n+2) | linken Bruch gleichnahmig machen, d.h. beide Nenner auf (n+2) erweitern
= 1 - 1 bzw. n * (n+2)/(n+1)*(n+2) + 1/(n+1)*(n+2) | beide Brüche auf einen Hauptnenner bringen
= 1 - 1 bzw. n * (n+2)/(n+1)*(n+2) | Zähler zusammenrechnen
= 1 - n^2 + 2n+1/(n+1)*(n+2) | 1. binomische Formel im linken Bruch bzw. Zähler
= 1 - (n+1)^2 + 1/(n+1)*(n+2) | (n+1) abkürzen
= 1 - (n+1) + 1/(n+2) ????????