Berechne die Entfernung der beiden Boote!

Question

Aufgabe:

von der 133m über einem See liegenden Spitze eines Hügels sieht man zwei Boote. Das eine erscheint im nördlichen Richtung unter dem Tiefenwinkel 39 Grad, das andere in östliche Richtung unter Tiefenwinkel 29 Grad.

Problem/Ansatz

Berechne die Entfernung der beiden Boote!

Answer 1

In dubio pro SKIZZE! :)

Answer 2

Wenn a die Entfernung des 1. Bootes vom Fußpunkt des Lotes von

der Spitze des Hügels auf Seeniveau ist und b für das 2. Boot, dann gilt

tan(29°) = a/h und tan(39°)=b/h

also a= 133m*tan(29°)= 73,72 m  entsprechend b=107,70m .

Die Differenz ist die Entfernung der Boote zueinander.

Comments

Die Differenz ist die Entfernung der Boote zueinander.

Mathe gut - Geographie schwach oder was ?

Edit : Sehe gerade : Mathe auch schwach.

---

Kommentare auch schwach.

---

Polemik schwächer, setzen. Alle beide.

Answer 3

Entfernung nördliches Boot vom Beobachter aus:

sin 39° = 133 m / Entfernung

Entfernung östliches Boot vom Beobachter aus:

sin 29° = 133 m / Entfernung

Entfernung der Boote voneinander:

\( \sqrt{(133/tan \, 39°)^2 + (133/tan \, 29°)^2} \)

Alles jeweils unter Vernachlässigung der Erdkrümmung.

Answer 4

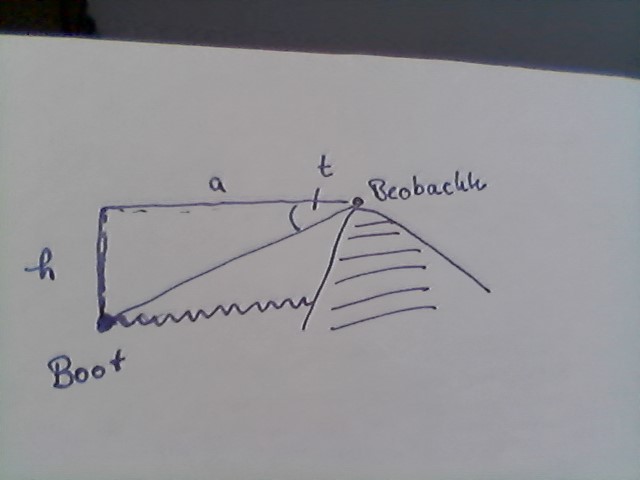
Selbst auf die Gefahr hin, Reem mit einer 3. Antwort völlig zu verwirren, versuche ich es mal:

Die Skizze zeigt mein Verständnis der Aufgabe: t ist der Tiefenwinkel und h = 133. Für das eine Boote ergibt sich:

$$\tan(39°)=\frac{h}{a} \Rightarrow a=\frac{h}{\tan(39°)}= 164$$

Für das andere Boot (korrigiert)

$$\tan(29°)=\frac{h}{b} \Rightarrow a=\frac{h}{\tan(29°)}= 240$$

Die Angabe "nördlich-östlich" bedeutet, dass die Blickrichtungen einen Winkel von 90° bilden, also die Linie zwischen den Booten als die Hypotenuse eines rechwinkligen Dreiecks mit Katheten a,b gesehen werden kann. Deren Länge ist:

$$\sqrt{a^2+b^2}=291$$

Gruß Mathhilf

Comments

Deren Länge ist:$$\sqrt{a^2+b^2}=286$$

Ein Problem des vorschnellen Rundens. Tatsächlich sind es mehr als 290 Meter.

---

Nee, ich habe mich schlicht verschrieben. Habe es gerundet korrigiert.

Danke für den Hinweis.

Gruß Mathhilf

---

Deren Länge ist:$$\sqrt{a^2+b^2}=291$$

Ein Problem des Rundens. Tatsächlich sind es weniger als 291 Meter.

---

Ja, aber da ich 3-stellig gearbeitet habe, ist die Abweichung im Rahmen.

Wenn man noch beachtet, dass das Boot nicht punktförmig sein dürfte, kann mit dieser Rundung leben - meine ich ;-)

Gruß Mathhilf

---

Sehe ich auch so, zumal man nicht weiß ob ich = ich ist.

---

Zumal ja nicht einmal klar ist, ob überhaupt nach der Entfernung der beiden Boote voneinander gefragt worden ist.

---

Guter Punkt, habe die Aufgabe nicht genau genug gelesen. Vielleicht auch Freudsche Fehlleistung: Warum die 2 Angaben, wenn man mit beiden doch nur das gleiche macht?

Gruß Mathhilf