z^4 + (2-2i)z^2 = 4i
(z^2+1-i)^2= 4i+(1-i)^2=4i+1-2i+i^2=2i | \( \sqrt{} \)
1.) z^2=i-1+\( \sqrt{2i} \)
..........
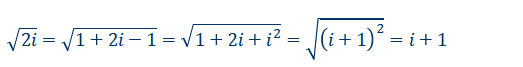
Text erkannt:
\( \sqrt{2 i}=\sqrt{1+2 i-1}=\sqrt{1+2 i+i^{2}}=\sqrt{(i+1)^{2}}=i+1 \)
1.) z^2=i-1+i+1 = 2i |\( \sqrt{} \)
z₁=\( \sqrt{2i} \)=i+1
z₂=-\( \sqrt{2i} \)=-i-1
2.) z^2=i-1-\( \sqrt{2i} \)=i-1-i-1=-2 |\( \sqrt{} \)
z₃=i*\( \sqrt{2} \)
z₄=-i*\( \sqrt{2} \)