Hallo, ich habe verschiedene AWP gegeben und soll die Lösungen für diese finden.
Ich habe nun zwei Lösungen für 2 Aufgaben und möchte gerne Feedback dazu erhalten da ich der Meinung bin das ich etwas falsch verstanden habe.
Die erste Zeile war jeweils gegeben und
gelöst habe ich die beiden Aufgaben nach dem Schema unten.
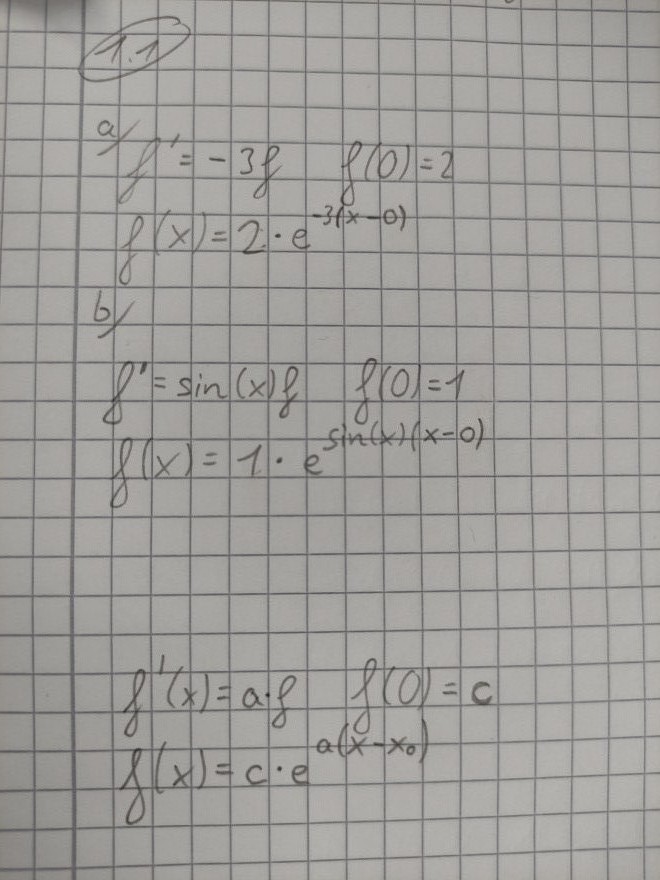
Text erkannt:
\( a^{\prime}=-3 f \quad f(0)=2 \)
\( f(x)=2 \cdot e^{-3(x-0)} \)
\( f^{\prime}(x)=a \cdot f \quad f(0)=c \)
\( f^{\prime}=\sin (x) f \quad f(0)=1 \)
\( f(x)=1 \cdot e^{\sin (x)(x-0)} \)
\( f(x)=c \cdot e^{a\left(x-x_{0}\right)} \)
Fällt etwa das x von sin (x) mit in die Klammer( x-x0)?