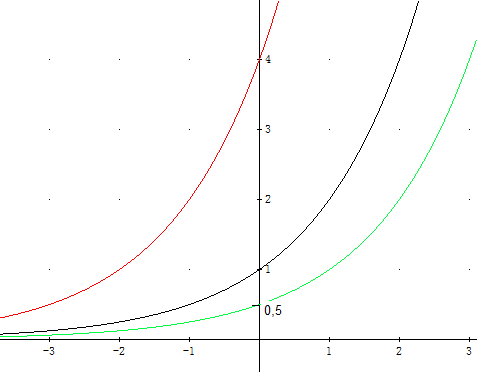
Schwarz: f(x)=2x
Rot: g(x)=2x+2
Grün: h(x)=0,5·2x
Betrachten wir zunächst nur die Schnittpunkte der drei Graphen mit der senkrechten Koordinatenachse, also f(0)=1, g(0)=4 und h(0)=,5. Hier gilt: h(0)=0,5·f(0) und g(0)=4·f(0). Denke dir dann eine Parallele zur senkrechten Achse an der Stelle x. Hier gilt h(x)=0,5·f(x) und g(x)=4·f(x). Der Rote Graph ist der gestreckte schwarze Graph und der Grüne Graph ist der gestauchte schwarze Graph.
Denke dir jetzt eine Parallele zur x-Achse, zum Beispiel y=1. hier ist f(0)=1, g(-2)=1 und h(1)=1. Rot ist gegenüber schwarz um 2 nach links verschoben. Grün ist gegenüber schwarz um 1 nach rechts verschoben.