Wo liegt der Fehler?
Durch einsetzen bekomme ich unterschiedliche Ergebnisse... (1. Zeile war vorgegeben)
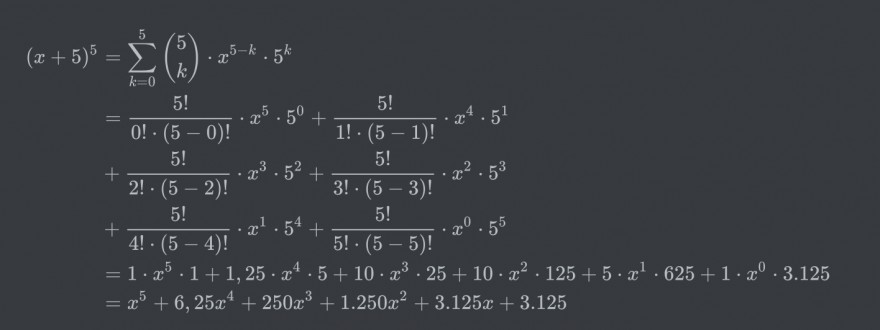
Text erkannt:
\( \begin{aligned}(x+5)^{5} &=\sum \limits_{k=0}^{5}\left(\begin{array}{l}5 \\ k\end{array}\right) \cdot x^{5-k} \cdot 5^{k} \\ &=\frac{5 !}{0 ! \cdot(5-0) !} \cdot x^{5} \cdot 5^{0}+\frac{5 !}{1 ! \cdot(5-1) !} \cdot x^{4} \cdot 5^{1} \\ &+\frac{5 !}{2 ! \cdot(5-2) !} \cdot x^{3} \cdot 5^{2}+\frac{5 !}{3 ! \cdot(5-3) !} \cdot x^{2} \cdot 5^{3} \\ &+\frac{5 !}{4 ! \cdot(5-4) !} \cdot x^{1} \cdot 5^{4}+\frac{5 !}{5 ! \cdot(5-5) !} \cdot x^{0} \cdot 5^{5} \\ &=1 \cdot x^{5} \cdot 1+1,25 \cdot x^{4} \cdot 5+10 \cdot x^{3} \cdot 25+10 \cdot x^{2} \cdot 125+5 \cdot x^{1} \cdot 625+1 \cdot x^{0} \cdot 3.125 \\ &=x^{5}+6,25 x^{4}+250 x^{3}+1.250 x^{2}+3.125 x+3.125 \end{aligned} \)