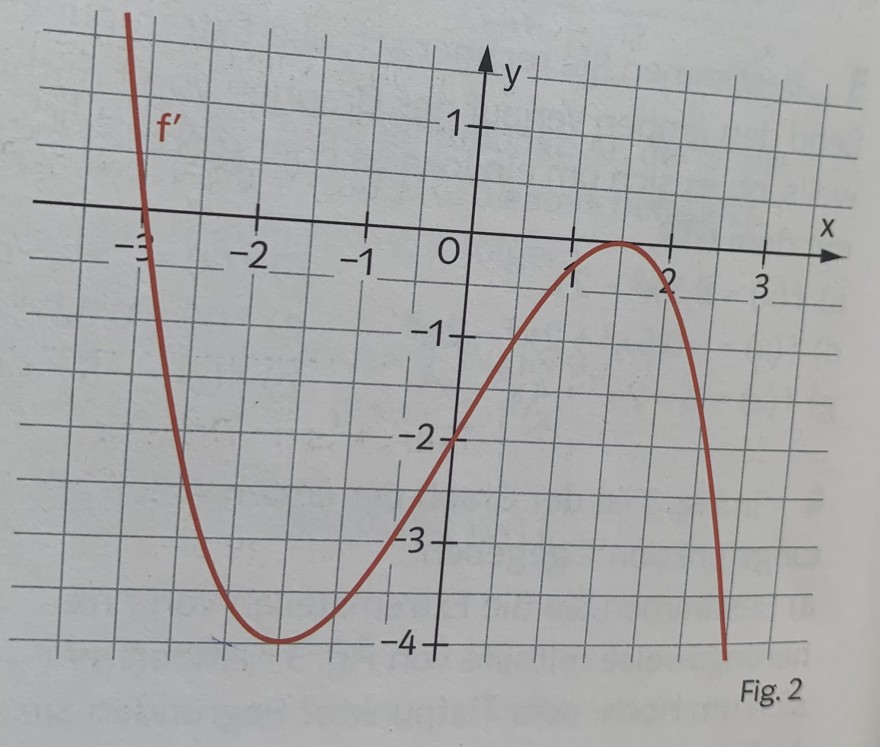
Gegeben ist der Graph der Ableitungsfunktion f‘ einer Funktion.
Welche der folgenden Aussagen sind wahr, welche falsch? Begründe.
a) f hat im Bereich -3,2< x < 3 zwei lokale extremwerte.
Frage: ist die Aussage falsch, weil es nicht extremwerte, sonder extremstellen heißt?
b) der Graph von f hat an der Stelle x=1,5 , einen Punkt mit waagerechter tangente, der weder hoch- noch Tiefpunkt ist.
Frage: Diese Aussage ist doch falsch, weil es an der Stelle x=1,5 einen vorzeichenwechsel gibt und somit ein hochpunkt?
c) an der Stelle x= -1,5 besitzt f‘‘ eine Nullstelle mit vorzeichenwechsel von + nach -
Frage: Wie komme ich von der ersten Ableitung auf die zweite Ableitung, wenn ich keine Funktionsgleichung angegeben habe?