Bei welchen Maßen des Plakats ist die bedruckte Fläche am größten?

Question

Aufgabe:

Ein rechteckiges Plakat hat eine Fläche von 35 dm².

Es wird so bedruckt, dass die Ränder an den Seiten jeweils 4 cm oben und unten jeweils 5 cm betragen. Bei welchen Maßen des Plakats ist die bedruckte Fläche am größten?

Problem/Ansatz:

Ich komme bei der Aufgabe nicht weiter. Ich weiß das die maximale Fläche gefragt ist. Aber mir fehlt der Ansatz. Und wie ungefähr würde die Skizze aussehen?

Comments

Vom Duplikat:

Titel: Bekomme diese Aufgabe nicht hin!?

Stichworte: extremwertaufgabe

Aufgabe:

Ein rechteckiges Plakat hat eine Fläche von 35 dm².

Es wird so bedruckt, dass die Ränder an den Seiten jeweils 4 cm oben und unten jeweils 5 cm betragen. Bei welchen Maßen des Plakats ist die bedruckte Fläche am größten?

Problem/Ansatz:

Kann mir jemand hier helfen?

---

Schau mal da :

https://www.mathelounge.de/833852/bei-welchen-massen-des-plakats-ist-bedruckte-flache-grossten?show=833868#a833868

Answer 1

Ein rechteckiges Plakat hat eine Fläche von 35 dm².

HB:

A(a,b)= (a-2*4)*(b-2*5) soll maximal werden.

NB:

a*b=35  → b=\( \frac{35}{a} \)

A(a)= (a-8)*(\( \frac{35}{a} \)-10)= 115 - 10a - \( \frac{8*35}{a} \)

A´(a)= - 10 +\( \frac{280}{a^2} \)

- 10 +\( \frac{280}{a^2} \)=0      \( \frac{28}{a^2} \)=1      a^2=28

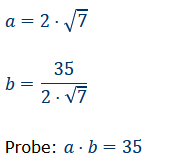
Text erkannt:

\( a=2 \cdot \sqrt{7} \)
\( b=\frac{35}{2 \cdot \sqrt{7}} \)
Probe: \( a \cdot b=35 \)

Comments

Wieso bei der HB a-2*4 .....?

---

Wie sind Sie auf die HB gekommen?

---

Wieso bei der HB a-2*4 .....?

Weil die Schrift an beiden Seiten je 4cm eingerückt wird.

---

"Wie sind Sie auf die HB gekommen?"

Die rote Fläche in der Skizze soll maximal werden.

---

Wie sind Sie auf die HB gekommen?

Interessanter ist die Frage : Warum liefert so eine schlampige Lösung dennoch (bei korrekter Interpretation) das richtige Ergbnis ?

---

Dich hält niemand ab, eine nicht schlampige Lösung zu schreiben.

---

Wie würdest du es machen?

---

Warum liefert so eine schlampige Lösung dennoch (bei korrekter Interpretation) das richtige Ergbnis ?

Weil es nicht auf das absolute Mass der Seitenränder ankommt, sondern lediglich auf ihr Verhältnis zu einander! Und das Verhältnis \(4\div 5\) bleibt konstant, auch wenn man beide Werte mit 10 (oder 2) multipliziert.

---

Meine Frage war natürlich nicht an dich gerichtet

---

Meine Frage war natürlich nicht an dich gerichtet

macht nix ;-)

geometrisch lässt sich das so interpretieren:

 (Maße in \(\text{dm}\))

Die Fläche des inneren Rechtecks ist genau dann maximal - bei gegebener Gesamtfläche - wenn die Diagonalen beider Rechtecke zusammen fallen.

Answer 2

Bedruckte Fläche A(a)=(a-4)·(b-5) oder A(a)=a·b-5b-5a+20 (Zielfunktion)

Nebenbedingung: a·b=35 oder b=\( \frac{35}{a} \).

Nebenbedingung in Zielfunktion einsetzen:

A(a)=35-\( \frac{175}{a} \)-5a+20

A'(a)=\( \frac{175}{a^2} \)-5

0=\( \frac{175}{a^2} \)-5 hat die positive Lösung a=√35.

Dann ist b=√35.

Comments

@Roland: die 4 und die 5 sind jeweils \(4\,\text{cm}\) und \(5\,\text{cm}\) und die Fläche ist \(35\,\text{dm}^2\).

Die Lösung ist \(a= 20\sqrt 7\, \text{cm}\) und \(b= 25\sqrt 7 \, \text{cm}\)