Aufgabe:
Sei
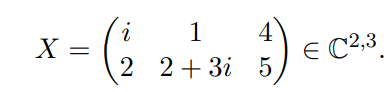
Text erkannt:
\( X=\left(\begin{array}{ccc}i & 1 & 4 \\ 2 & 2+3 i & 5\end{array}\right) \in \mathbb{C}^{2,3} \)
Bestimmen sie XH und berechnen sie XH X.
.
Problem/Ansatz:
Ich verstehe nicht wie ich die hermitesche Matrix bestimmen soll, da diese keine quadratische Matrix ist, ist das doch nicht möglich oder?