Hallo Mercelo,
Du hast leider die Klassenstufe nicht angegeben, denn es gibt schon mehrere hundert Jahre Forschung auf diesem Gebiet!
Den Faktor kann man weglassen -> siehe https://de.wikipedia.org/wiki/Nullteiler#Satz_vom_Nullprodukt
a) Das "Rumprobieren" wird leider immer noch gelehrt, obwohl es schon über 400 Jahre veraltet ist. Da es hier aber eine "Glatte Nullstelle" gibt, sieht es genau danach aus, dass der Aufgabensteller sich genau so einen seltenen Spezialfall herausgesucht hat.Die restlichen Nullstellen bekommt man oft nach Polynomdivision und quadratischer Gleichung heraus. Wenn ihr noch keine komplexen Zahlen hattet, brauchst Du wegen des negativen Arguments innerhalb der Wurzel nicht weitermachen -> es gibt "für Euch" dann nur 1 reelle Nullstelle.
b) https://de.wikipedia.org/wiki/Bisektion oder Intervallhalbierung -> ist eigentlich "systematisches Probieren" im abgesteckten Suchbereich.
c) Über 300 Jahre gibt es schon das https://de.wikipedia.org/wiki/Newtonverfahren
Dazu müsst Ihr die Ableitung behandelt haben.
Der Iterationsrechner unter http://www.gerdlamprecht.de/Roemisch_JAVA.htm Beispiel 118 rechnet das online vor:
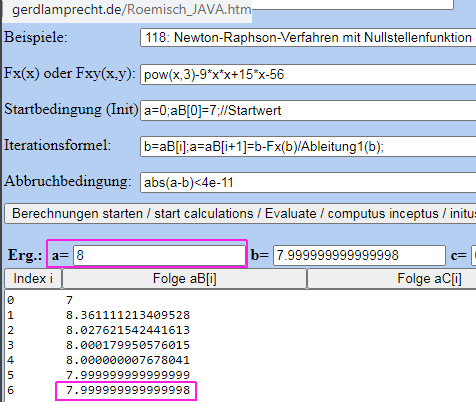
Hinweis: x*x*x = x³ = x^3 = pow(x,3)
d) die https://de.wikipedia.org/wiki/Cardanische_Formeln gibt es auch schon über 400 Jahre. Sind aber kompliziert und haben Fallunterscheidung.
e) aus d) kann man mit Hilfe der komplexen Zahlen die Fallunterscheidungen eliminieren und bekommt die exakte PQRST-Formel (analog zur pq-Formel bei Polynomen Grad 2):
https://www.lamprechts.de/gerd/Bilder/QuadratischeGleichung_p-q-Formel_KubischeGleichung_PQRST-Formel.png
Also einfach Zahlenwerte einsetzen & ausrechnen -> das kann jede "dumme Maschine", die mit komplexen Zahlen rechnen kann. Bei Lehrern nicht bekannt, da es kein https://de.wikipedia.org/wiki/Lehrstoff ist.
Der Nullstellenrechner unter https://www.lamprechts.de/gerd/php/gleichung-6-grades.php
rechnet e) & d) online mit Zwischenergebnissen vor:
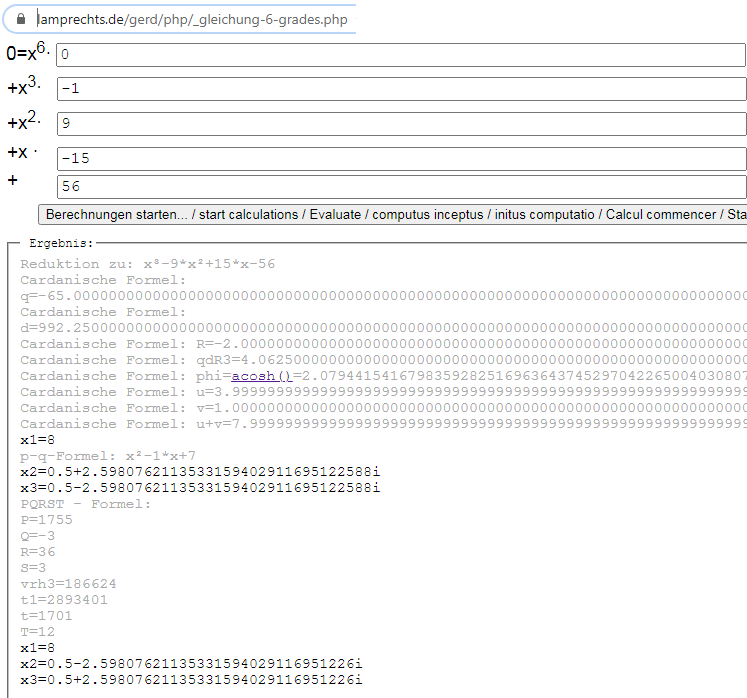
f) Nur für Interessierte: es gibt noch hypergeometrische Funktionen, wo man einige Nullstellen DIREKT berechnen kann:
http://www.gerdlamprecht.de/Explizite-Loesungsformeln-fuer-Polynome-hypergeometrische-Funktion.htm