Berechnen Sie das Volumen V.

Question

Aufgabe:

Gegeben sei das Gebietsintegral V =∫f (x , y)d A = \( \int\limits_{0}^{1} \)
                                                        B

\( \int\limits_{x}^{x+1} \) xy dy dx

Skizzieren und schraffieren Sie den Integrationsbereich B in xy-Darstellung!
Berechnen Sie das Volumen V.

Answer 1

Aloha :)

Die Menge \(B=\{(x|y)\in\mathbb R^2\,\big|\,0\le x\le 1\;\land\;x\le y\le x+1\}\) ist ein Parallelogramm:

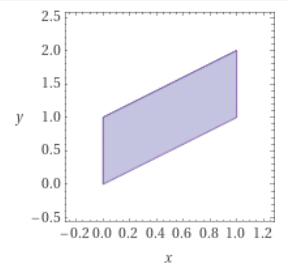
Das gesuchte Volumen lässt sich wie folgt berechnen:

$$V=\iint\limits_Bxy\,dA=\int\limits_0^1dx\int\limits_x^{x+1}dy\, x\cdot y=\int\limits_0^1dx\,x\int\limits_x^{x+1}dy\,y=\int\limits_0^1dx\,x\left[\frac{y^2}{2}\right]_{y=x}^{x+1}$$$$\phantom{V}=\int\limits_0^1dx\,\frac{x}{2}\left((x+1)^2-x^2\right)=\int\limits_0^1dx\left(x^2+\frac{x}{2}\right)=\left[\frac{x^3}{3}+\frac{x^2}{4}\right]_0^1=\frac{1}{3}+\frac{1}{4}=\frac{7}{12}$$