Steckbriefaufgabe (Parabel 2. Ordnung)

Question

Hallo, ich muss die Matrix aufstellen von den zwei Punkten einer Parabel 2. Ordnung:

Hochpunkt (0/5)--> 4a+2b+c= -3

Tiefpunkt (2/-3)----> c=0

muss ich noch eins der Punkte ableiten,um die Matrix aufstellen zu können?

:)

Comments

Ist wohl eher eine Parabel 3. Ordnung ?

Answer 1

Ich weiß nicht, was das mit einer Matrix zu tun hat.

Ich würde so rechnen:

f(x)=ax^2+bx+c

f'(x)=2ax+b

(0|5) Kurvenpunkt: c=5

(0|5) Hochpunkt: b=0

(2|-3) Kurvenpunkt: -3=a*4+5 → a=-2

f(x)=-2x^2+5

:-)

Answer 2

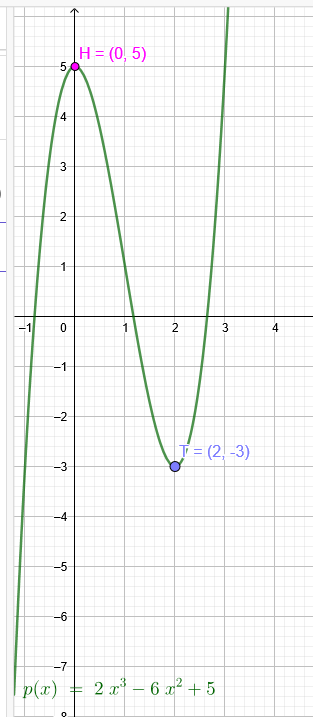
Ich gehe auch von einer Parabel 3.Grades aus:

H (0|5)  →H´(0|0)

T (2|-3)  →T´ (2|-8) 

H´(0|0):

f(x)=a*x^2*(x-N)

T´ (2|-8):

f(2)=4a(2-N)

4a(2-N)=-8 → 8a-4aN=-8  →  a*(8-4N)=-8   

f(x)=\( \frac{8}{4N-8} \)[x^2*(x-N)]

Extremwerteigenschaft:

f´(x)=\( \frac{8}{4N-8} \)[2x*(x-N)+x^2]

f´(2)=\( \frac{8}{4N-8} \)[4*(2-N)+4]

\( \frac{8}{4N-8} \)[4*(2-N)+4]=0

4*(2-N)+4=0→2-N+1=0→   N=3    → a=2

f(x)=2[x^2*(x-3)]=2x^3-6x^2

Gesuchte Parabel:

p(x)=2x^3-6x^2+5