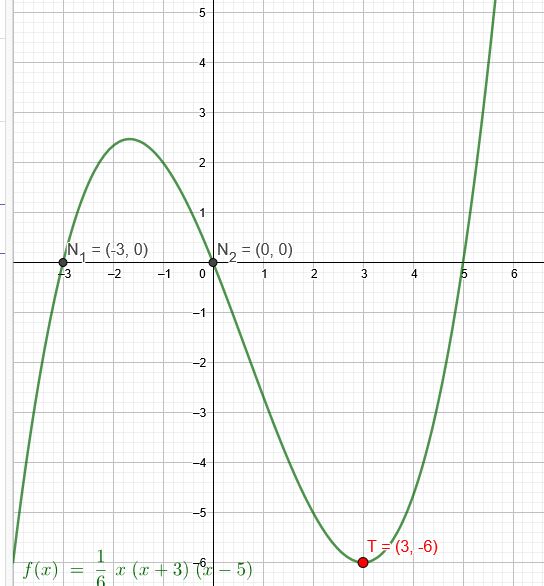
" 0 und -3 sind Nullstellen, E (3|-6) ist relativer Tiefpunkt (Hochpunkt)" (3.Grad)
\(f(x)=a*x*(x+3)*(x-N)\)
\(E (3|-6)\)
\(f(3)=a*3*(3+3)*(3-N)=18a*(3-N)\)
\(18a*(3-N)=-6\) → \(3a*(N-3)=1\) → \(3a*(N-3)=1\) → \(a=\frac{1}{3N-9}\)
\(f(x)=\frac{1}{3N-9}*(x^2+3x)*(x-N)\)
relativer Tiefpunkt (Hochpunkt):
\(f´(x)=\frac{1}{3N-9}*[(2x+3)*(x-N)+(x^2+3x)*1]\)
\(f´(3)=\frac{1}{3N-9}*[(2*3+3)*(3-N)+(3^2+3*3)]\)
\(\frac{1}{3N-9}*[(2*3+3)*(3-N)+(3^2+3*3)]=0\)
\(N=5\) \(a=\frac{1}{3*5-9}=\frac{1}{6}\)
\(f(x)=\frac{1}{6}*x*(x+3)*(x-5)\)
Mit relativem Hochpunkt geht es nicht.