32-\( 0,5^{2x} \) -12+3=-28*\( 0,5^{x} \)
23-\( 0,5^{2x} \) =-28*\( 0,5^{x} \) u=\( 0,5^{x} \)
23-u^2=-28*u
u^2-28u=23
(u-14)^2=23+14^2=219|\( \sqrt{} \)
1.)u-14=\( \sqrt{219} \)
u₁=14+\( \sqrt{219} \)
Resubstitution:
14+\( \sqrt{219} \)=\( 0,5^{x} \)|ln
ln(14+\( \sqrt{219} \))=x*ln0,5
x₁=ln(14+\( \sqrt{219} \))/ln0,5
2.)u-14=-\( \sqrt{219} \)
u₂=14-\( \sqrt{219} \)
x₂=ln(14-\( \sqrt{219} \))/ln0,5 Aufpassen bei ln(-...)!
Text erkannt:
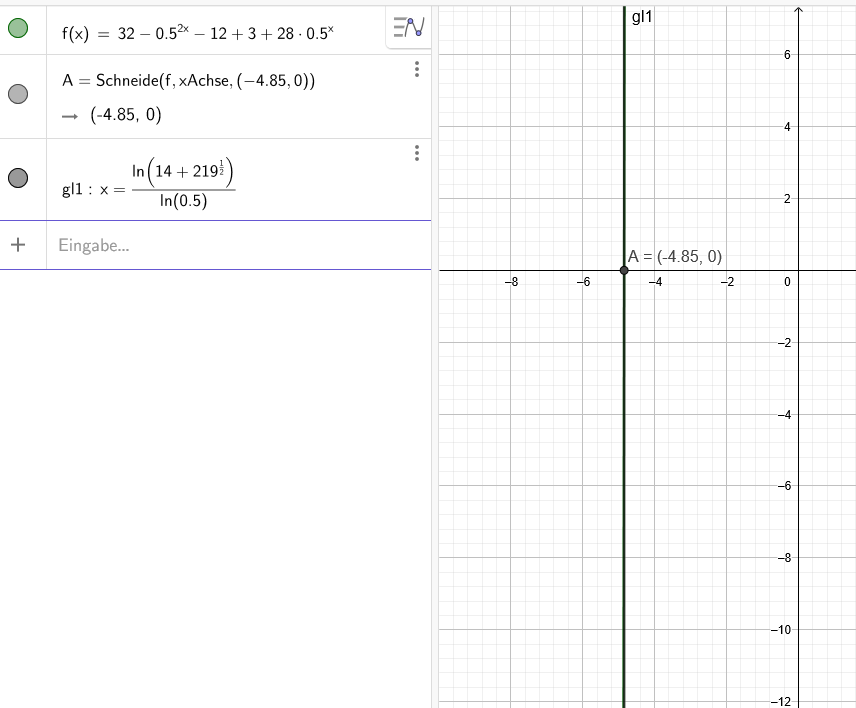
\( f(x)=32-0.5^{2 x}-12+3+28 \cdot 0.5^{x} \)
\( \mathrm{A}=\operatorname{Schneide}(\mathrm{f}, \times \) Achse,\( (-4.85,0)) \)
\( \rightarrow(-4.85,0) \)
\( \mathrm{g} 11: \mathrm{x}=\frac{\ln \left(14+219^{\frac{1}{2}}\right)}{\ln (0.5)} \)
\( +\quad \) Eingabe...