Aufgabe:
Folgende Vektoren sind gegeben:
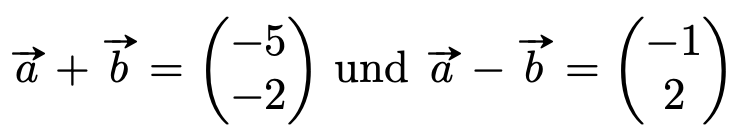
Text erkannt:
\( \vec{a}+\vec{b}=\left(\begin{array}{l}-5 \\ -2\end{array}\right) \) und \( \vec{a}-\vec{b}=\left(\begin{array}{c}-1 \\ 2\end{array}\right) \)
Man soll die Vektoren a und b berechnen.
Problem/Ansatz:
Wie geht man hier vor?
Mein Ansatz war, dass ich a+b einzeichne und dann die Vektoren a und b ablese.
D.h. für a+b: a = (0,-2); b=(-5,9)
und für a-b: a= (-1,2) b=(0,0)
Kann das stimmen? Bin mir ziemlich unsicher.
Stimmt das?