Bestimmen Sie eine Matrix mit der Eigenschaft X^-1=B*A

Question

Aufgabe:

Text erkannt:

Aufgabe 5: Matrizen
Gegeben seien die Matrizen
\( A=\left[\begin{array}{lll}6 & 4 & 1 \\ 5 & 7 & 3 \\ 1 & 2 & 1\end{array}\right] \) und \( B=\left[\begin{array}{ccc}-3 & 0 & 1 \\ -2 & 1 & 2 \\ 1 & -2 & 1\end{array}\right] \)
Bestimmen Sie eine Matrix \( \mathrm{X} \) mit der Eigenschaft \( X^{-1}=B \cdot A \)

Problem/Ansatz:

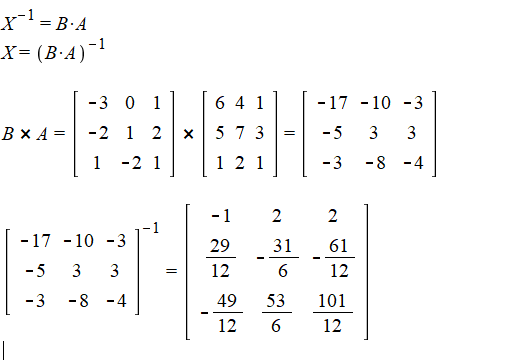
Text erkannt:

\( X^{-1}=B \cdot A \)
\( X=(B \cdot A)^{-1} \)
\( B \times A=\left[\begin{array}{ccc}-3 & 0 & 1 \\ -2 & 1 & 2 \\ 1 & -2 & 1\end{array}\right] \times\left[\begin{array}{lll}6 & 4 & 1 \\ 5 & 7 & 3 \\ 1 & 2 & 1\end{array}\right]=\left[\begin{array}{ccc}-17 & -10 & -3 \\ -5 & 3 & 3 \\ -3 & -8 & -4\end{array}\right] \)
\( \left[\begin{array}{ccc}-17 & -10 & -3 \\ -5 & 3 & 3 \\ -3 & -8 & -4\end{array}\right]^{-1}=\left[\begin{array}{ccc}-1 & 2 & 2 \\ \frac{29}{12} & -\frac{31}{6} & -\frac{61}{12} \\ -\frac{49}{12} & \frac{53}{6} & \frac{101}{12}\end{array}\right] \)

Ist dieser Lösungsansatz korrekt?
Wie löse ich die Matrizengleichung nach X auf?

Gruß Jan

Answer 1

Hallo,

der Lösungsansatz ist korrekt. Multipliziere beide Seiten von rechts mit \(X\) und dann von links mit \((BA)^{-1}\). Dann gilt:$$X^{-1}=BA \Rightarrow E=(BA)X \Rightarrow X=(BA)^{-1}$$

Comments

Hallo,

ja, ich muss auf beiden Seiten der Gleichung mit X multiplizieren und dann nach X auflösen.

Vielen Dank für die schnelle Antwort.

Gruß Jan

---

Matrizenmultiplikation ist nicht kommutativ, daher ist es ausschlaggebend ob du mit dem rechts- oder linksinversen Element multiplizierst. Ist hier nicht zwingend wichtig, da \(AE=EA\) ist, aber normalerweise ist diese Kommutativität nicht gegeben.

VG