Berechne die Seitenlängen.

Question

Aufgabe: Ein Rechteck hat den Flächeninhalt 20cm². Die Diagonalen schneiden sich unter einem Winkel von 40 grad. Berechne die Seitenlängen.

Problem/Ansatz:  Ich verstehe die Aufgabe nicht, alles was ich bisher hab ist

x=1.36a (x ist der umfang)

und nichtmal da weiß ich ob es richtig ist, Kann mir bitte jemand die Lösung sagen?

Answer 1

Hallo Sophie,

wenn der Winkel der beiden Diagonalen des Rechtecks \(=40°\) ist (blau), ...

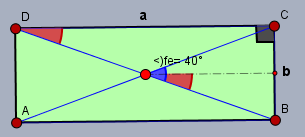
... dann ist der WInkel zwischen der Diagonalen \(AC\) zur Seite \(DC\) genau halb so groß (der rote Winkel). Aus den rechtwinkligen Dreieck \(\triangle DBC\) kann man ablesen:$$\tan \left(\frac{40°}2\right) = \frac {b}{a} \implies b = a \cdot \tan\left( 20°\right)$$Bekanntermaßen ist die Fläche \(F\) des Rechtecks$$F = a \cdot b = 20\,\text{cm}^2$$Setzt man dort das \(b\) ein, folgt daraus$$\begin{aligned}a \cdot b &= 20\,\text{cm}^2 \\ a \cdot a \cdot \tan\left( 20°\right) &= 20\,\text{cm}^2 \\ a^2 &= \frac{20\,\text{cm}^2 }{\tan\left( 20°\right)} \\ a &= \sqrt{\frac {20}{\tan(20°)}} \text{cm} \approx 7,41\,\text{cm} \end{aligned}$$und \(b\) ist dann$$b = a \cdot \tan(20°) \approx 2,70\,\text{cm}$$

Comments

dankeschön, ich habe es grade auch ausgerechnet und für a habe ich 6√5/5 und für b habe ich 10√5/3, Ist das gleiche oder?

---

für a habe ich 6√5/5 und für b habe ich 10√5/3, Ist das gleiche oder?

Nein - ist nicht das gleiche! Der Winkel \(\angle BDC\) (der rote s.o.) wäre dann$$\angle BDC = \arctan\left( \frac{6 \frac{\sqrt 5}{5}}{10 \frac{\sqrt 5}{3}}\right) \\ \phantom{\angle BDC} = \arctan\left( 0,36 \right) \approx 19,8° \ne \frac{40°}2$$wenn Du schreibst, dass $$a = \frac 65 \sqrt 5$$dann suggerierst Du, dass es sich um ein exaktes Ergebnis handelt. Das ist hier nicht der Fall!$$a \approx 2,7$$wäre dagegen völlig in Ordnung.

---

PS.: wenn Du statt \(x=1,36a\) besser$$x \approx \frac{15}{11} a$$wählst, kommst Du wesentlich besser hin ;-) Der Fehler, den Du dann machst, wäre dann nur noch ein Zehntel von dem Fehler, den Du bei \(x=1,36a\) machst.